8. Statistical Physics

8.1. Historical Overview

At the beginning of the 19th century, many scientists had a mechanistic view of the universe containing a well-regulated and wholly deterministic set of physical laws. This was in large part due to the success of Newtonian physics up to that point. New mathematical models from Lagrange (~1790) and Hamilton (~1840) added to the computational power of Newtonian mechanics, which enabled physicists to describe complex physical systems with 2nd order differential equations.

Pierre-Simon de Laplace held that it should be possible (in principle) to have a perfect knowledge of the physical universe. This knowledge was dependent on the precision of measuring the position and velocity of every particle of matter and applying Newton’s laws. The Heisenberg uncertainty principle creates serious problems for this position.

Note

Laplace did make major contributions to probability theory despite having a firm belief in a completely deterministic universe. His study of probability may have been inspired to test the practical limits of measurement in classical mechanics.

The development of statistical physics in the 19th century was in tandem with the development of thermodynamics. At this time, the calorie was considered a fluid that could flow through bodies to effect changes in temperature. In 1798, Benjamin Thompson suggested that heat is merely the motion of individual particles in a substance. He was ahead of his time in this idea and in the way of demonstrating it. In 1822, Joseph Fourier published his theory of heat, which was the first truly mathematical treatise on the subject. It was a non-statistical, quantitative basis for later work.

The concept of energy is central to modern thermodynamics, where James Prescott Joule demonstrated the mechanical equivlalent of heat in 1843. He showed that the energy of a falling weight to turn a paddle wheel through water would transfer into the water itself.

James Clerk Maxwell brought the mathematical theories of probability and statistics to bear on thermodynamics. Maxwell derived expressions for the distribution of velocities in an ideal gas and used these distributions to derive the observed macroscopic phenomena. In thermodynamics, he believed that all relevant properties were due to the motions of individual particles.

In the early 20th century, Einstein published his theory of Brownian (random) motion, which helped support the atomic view of matter. Jean Baptiste Perrin would confirm Einstein’s results through his experiments. Soon after, Bohr developed his atomic model, which led to the development of quantum theory.

Some people have difficulty accepting the probablistic nature of statistical physics, where they perceive a lack of determinism. No less a figure than Einstein worried about this. He said, “God does not play dice,” which implied that some causal mechanism (beyond our understanding) must be at work. Statistical physics is necessary regardless of the ultimate nature of reality. This is true for at least three reasons:

1. The problem of determining the outcome of a coint toss is so complex that it is most often useful to reduce it to statistical terms. It depends on air resistance, rotational dynamics, and restitution that make predicting the outcome a formidable mechanics problem.

2. When the number of pariticles is large (e.g., Avogadro’s number large), it is highly impractical to study individual particles if only a description of the overall behavior is desired (e.g., pressure, temperature, or specific of an ideal gas).

3. Uncertainties are inherent in physics, and they are significant enough to affect atomic and subatomic systems.

8.2. Maxwell Velocity Distribution

To know everything about an ideal gas, we need to describe the state of the gas at a given time. This state can be defined using six parameters per particle consisting of three for position \((x,\ y,\ z)\) and three for velocity \((v_x,\ v_y,\ v_z)\). Many relevant quantitities must depend on one (or more) of these six parameters. These parameters are also described as the componenets of a 6-D phase space.

Maxwell focused on the thee velocity components because the energy of a gas should depend only on the velocities and not the instantaneous positions (i.e., \(K = 1/2mv^2\)). The crucial question for Maxwell was:

What is the distribution of velocities for an ideal gas at a given temperature?

To begin, we define a velocity distribution function \(f(\vec{v})\) such that

\[\begin{align*} f(\vec{v})\ d^3\vec{v} =& \text{ the probability of finding a particle with}\\ & \text{a velocity between }\vec{v}\ \text{and}\ \vec{v} + d^3\vec{v}, \end{align*}\]

where \(d^3\vec{v} = dv_x\ dv_y\ dv_z\), or a volume element in the phase space. The product of a velocity distribution funciton with a phase space volume plays a role analogous to the probability density \(\Psi^*\Psi\) in quantum theory.

Maxwell proved that the probability distribution funciton is proportional to \(e^{-mv^2/(2kT)}\), where \(m\) is the molecular mass, \(v\) is the molecular speed, \(k\) is Boltzmann’s constant, and \(T\) is the absolute temperature. Then, we may write

(8.1)\[\begin{align} f(\vec{v})\ d^3\vec{v} = Ce^{-\frac{1}{2}\beta mv^2}\ d^3\vec{v}, \end{align}\]

where \(C\) is aproportionality factor and \(\beta \equiv (kT)^{-1}\); not to be confused with \(\beta = v/c\) from relativity. We can expand the above expression as

(8.2)\[\begin{align} f(\vec{v})\ d^3\vec{v} = Ce^{-\frac{1}{2}\beta m(v_x^2+v_y^2+v_z^2)}\ d^3\vec{v}, \end{align}\]

and use the properties of exponents to rewrite as three factors that each contain one of the three velocity components. They are defined as

(8.3)\[\begin{align} g(v_x)\ dv_x &\equiv C^\prime e^{-\frac{1}{2}\beta mv_x^2}\ dv_x, \\ g(v_y)\ dv_y &\equiv C^\prime e^{-\frac{1}{2}\beta mv_y^2}\ dv_y, \\ g(v_z)\ dv_z &\equiv C^\prime e^{-\frac{1}{2}\beta mv_z^2}\ dv_z, \end{align}\]

with a new constant \(C^\prime = C^{1/3}\).

We need to know the value of \(C^\prime\). Given that \(g(v_x)\ dv_x\) is the probability that a gas particles’s \(x\)-velocity lies in an interval of \(v_x\) and \(v_x + dx\), we can sum (or integrate) over all possible values. The sum of all probabilities is equal to unity because every molecule has an \(x\)-velocity wihtin that range. This is similar to the reasoning for the process of normalization from quantum theory.

Integration of Probability Integrals

The integral becomes

\[\begin{align*} \int_{-\infty}^\infty g(v_x)\ dv_x &= C^\prime \int_{-\infty}^\infty e^{-\frac{1}{2}\beta mv_x^2}\ dv_x, \end{align*}\]

where only half the interval is evaluated and multiplied by two due to the properties of an even function.

If we multiply both sides by \(v_x\), then the integrand becomes an odd function and the two parts would cancel. To avoid the trivial solution (i.e., symmetric integral of an odd function), we integrate only the positive values as

\[\begin{align*} I_n &= C^\prime \int_{0}^\infty v_x e^{-\frac{1}{2}\beta mv_x^2}\ dv_x, \\ & = C^\prime \int_{0}^\infty u e^{-a u^2}\ du, \end{align*}\]

where \(u = v_x\) and \(a=\beta m/2\). Then, we can generalize (using even and odd powers of \(u\)) to say

\[\begin{align*} \int_{-\infty}^\infty u^n e^{-au^2}\ du &= \begin{cases} 2I_n & \text{for even }n, \\ 0 & \text{for odd }n. \end{cases} \end{align*}\]

Starting with \(n=0\), we have

(8.4)\[I_o = \int_0^\infty e^{-au^2}du.\]

This integral requires a dummy substitution, where we can find the product of two integrals \((u\rightarrow x,\ u\rightarrow y)\) that can be tranformed into polar coordinates. This leads to

\[\begin{align*} I_o^2 &= \int_0^\infty \int_0^\infty e^{-a(x^2+y^2)}\ dx\ dy, \\ &= \int_0^\infty e^{-ar^2}\ rdr \int_0^{\pi/2}d\theta. \end{align*}\]

We can easily evaluate the \(\theta\) integral, which yields \(\pi/2\) and the \(r\) integral can be evaluated using a standard substitution \((u=ar^2)\). We find that

(8.5)\[\begin{split}I_o^2 &= \frac{\pi}{4a} \int_0^\infty e^{-u}\ du = \frac{\pi}{4a}, \\ I_o &= \sqrt{\frac{\pi}{4a}} = \frac{1}{2}\sqrt{\frac{\pi}{a}}.\end{split}\]

This process can be expanded for other probability integrals, but we can now use the result for \(I_o\) to say

\[\begin{align*} \int_{-\infty}^\infty g(v_x)\ dv_x &= C^\prime \int_{-\infty}^\infty e^{-\frac{1}{2}\beta mv_x^2}\ dv_x,\\ &= C^\prime 2I_o = 1. \end{align*}\]

Recalling that \(a=\beta m/2\), we have

(8.6)\[\begin{align} C^\prime &= \frac{1}{2}\sqrt{\frac{4a}{\pi}}, \\ &= \frac{1}{2}\sqrt{\frac{2\beta m}{\pi}} = \sqrt{\frac{\beta m}{2\pi}}, \end{align}\]

and

(8.7)\[\begin{align} g(v_x)\ dv_x = \sqrt{\frac{\beta m}{2\pi}} e^{-\frac{1}{2}\beta mv_x^2}\ dv_x. \end{align}\]

With this distribution we can calculate \(\bar{v}_x\) (mean value of \(v_x\)) as

(8.8)\[\begin{align} \bar{v}_x = \int_{-\infty}^\infty v_x\ g(v_x)\ dv_x = C^\prime \int_{-\infty}^\infty v_x e^{-\frac{1}{2}\beta mv_x^2}\ dv_x = 0 \end{align}\]

because \(v_x\) is an odd function. The result makes sense because in a random distribution of velocities one woul expect the velocity components to be evenly distributed about \(v_x = 0\). The mean value of \(v_x^2\) is

(8.9)\[\begin{align} \bar{v}_x^2 &= \int_{-\infty}^\infty v_x^2\ g(v_x)\ dv_x, \\ &= 2C^\prime \int_{0}^\infty v_x^2 e^{-\frac{1}{2}\beta mv_x^2}\ dv_x. \end{align}\]

The integral can solved solved by differentiating \(I_o\) (Eq. (8.4)) with respect to \(a\) as

\[\begin{align*} \frac{dI_o}{da} = -\int_0^\infty u^2 e^{-au^2}du = -I_2, \end{align*}\]

or using Eq. (8.5) by

\[\begin{align*} I_2 = -\frac{dI_o}{da} = -\frac{\sqrt{\pi}}{2}\frac{d}{da}\left[a^{-1/2}\right] = \frac{\sqrt{\pi}}{4}a^{-3/2}. \end{align*}\]

Alternatively, one could use an integral table with exponential functions. The final result via substitution is

(8.10)\[\begin{align} \bar{v}_x^2 &= 2C^\prime I_2 = 2 \left(\frac{\beta m}{2\pi}\right)^{1/2} \frac{\sqrt{\pi}}{4}\left(\frac{2}{\beta m}\right)^{3/2}, \\ &= \frac{1}{\beta m} = \frac{kT}{m}. \end{align}\]

There’s nothing special about the \(x\)-direction, so the results for the \(x\)-, \(y\)-, and \(z\)-velocity components are identical. The three components can be summed to find the mean translational kinetic energy \(\overline{K}\) of a molecule:

(8.11)\[\begin{align} \overline{K} = \frac{1}{2}m \left(\bar{v}_x^2 + \bar{v}_y^2 + \bar{v}_z^2\right) = \frac{1}{2}m \left(\frac{3kT}{m}\right) = \frac{3}{2}kT. \end{align}\]

This is one of the principal results of kinetic theory.

Exercise 8.1

Compute the mean translational kinetic energy at room temperature \((293\ K)\) of:

(a) a single ideal gas molecule in \(\rm eV\), and (b) a mole of ideal gas in \(\rm J\).

(a) The mean kinetic energy of a single molecule is straigthforward where we substitute for \(T=293\ {\rm K}\). We can use the scipy.constants module to provide a value for the Boltzmann’s constant \(k\) in \(\rm eV/K\) so that we need to convert later. The mean kinetic energy is given as

\[ \overline{K} = \frac{3}{2}\left(8.617333262 \times 10^{-5}\ {\rm ev/K}\right)(293\ K) = 0.0379\ {\rm eV}. \]

The mean translational kinetic energy of a single ideal gas molecule is \(0.0379\ {\rm eV}\).

(b) For an entire mole, it’s necessary to multiply the result of the previous calculation by Avogadro’s number (i.e., the number of atoms in a mole). However, we must use the form of Boltzmann’s constant in \(\rm J/K\) instead. The mean kinetic energy in a mole is given as

\[ \overline{K} = \frac{3}{2}\left(1.380649 \times 10^{-23}\ {\rm J/K}\right)(293\ K) \times \left(6.02214076 \times 10^{23} \right) = 3650\ {\rm J}. \]

The mean translational kinetic energy of a whole mole of ideal gas molecules is \(3650\ {\rm J}\).

import numpy as np
from scipy.constants import physical_constants, Avogadro

Temp_room = 293 #room temperature in K
k_eV = physical_constants['Boltzmann constant in eV/K'][0]
k_J = physical_constants['Boltzmann constant'][0]

#Part (a)
Kmean = 1.5*k_eV*Temp_room
print("The mean kinetic energy of a single ideal gas molecule is %1.4f eV." % Kmean)

#Part(b)
Kmean = 1.5*k_J*Temp_room*Avogadro
print("The mean kinetic energy of a mole of ideal gas is %i J." % np.round(Kmean,-1))

The mean kinetic energy of a single ideal gas molecule is 0.0379 eV.
The mean kinetic energy of a mole of ideal gas is 3650 J.

8.3. Equipartition Theorem

In the previous section, we showed that the internal energy of a thermodynamic system can be related to its temperature. More precisely,

\[\begin{align*} \frac{1}{2}m\bar{v}_x^2 = \frac{1}{2}kT. \end{align*}\]

Similarly, there is an average energy associated with the other two velocity components, which produces a net average energy per molecule of \(\frac{3}{2}kT\). In a monatomic gas (e.g., \(\rm He\) or \(\rm Ar\)), virtually all of the energy is in the translational kinetic energy.

Rigid rotator model

Consider a diatomic gas (e.g., \(\rm O_2\)) as two atoms connected by a massless rod (i.e., a rigid rotator). Then the molecule can have rotational kinetic energy in addtion to translational kinetic energy. The crucial questions are:

1. How much rotational energy is there?

2. How is the rotational energy related to temperature?

These questions are answered by the equipartition theorem, which summarizes the ways that we can count up the different sources of energy.

In equilibrium there is a mean energy of \(\frac{1}{2}kT\) per molecule associated with each independent quadratic term in the molecule’s energy.

Independent quadratic terms could be present with respect to the coordinates, translational velocities, angular velocities, or anything else when squared is propotional to energy. Each independent phase space coordinate is called a degree of freedom.

Applying the equipartition theorem to a rigid rotator (e.g., \(\rm O_2\)) can help us identify additional sources of kinetic energy that we need to consider. The rotator is free to rotate about 2 independent axes. Let’s say that the rotator is aligned along the \(z\)-axis and then it can rotate about either the \(y\)- or \(x\)-axis. The corresponding rotational energies can be written in terms of rotational inertia and angular velocity,

\[\begin{align*} K_x &= \frac{1}{2}I_x\omega_x^2, \\ K_y &= \frac{1}{2}I_y\omega_y^2. \end{align*}\]

Each of these rotational energies \((K_x\ \text{or}\ K_y)\) is quadratic in angular velocity, so the equipartition theorem instructs us to add \(2\left(\frac{1}{2}kT\right) = kT\) per molecule to the translational kinetic energy for a total of \(\frac{5}{2}kT\).

Spring model

Sometimes it is a better approximation to think of atoms connected by a massless spring rather than a rigid rod. In this model, we use the potential energy of a spring but in radial coordinates:

\[ U = \frac{1}{2}\kappa \left(r-r_o \right)^2, \]

where \(\kappa\) is the spring’s force constant, \(r\) the separation between atoms, and \(r_o\) is the equlitbrium separation. This potential energy adds another quadratic (degree of freedom) to the total energy, where another degree of freedom is associated with the vibrational velocity, \(dr/dt\). This velocity contributes a vibrational kinetic energy as \(\frac{1}{2}m\left(\frac{dr}{dt}\right)^2\).

If the molecule is still free to rotate, there is now a total of seven degrees of freedom: 3 translational, 2 rotational, and 2 vibrational. The resulting average kinetic energy is \(\frac{7}{2}kT\).

How can we check our calculations? This is done by measuring the heat capacity of a gas at constant volume. In a gas of \(N\) molecules, the total internal energy should be

\[ U = N\overline{E} = \frac{f}{2}NkT, \]

where \(f\) indicates the degrees of freedom. The heat capacity at constant volume is

\[\begin{align*} C_{\rm V} &= \frac{f}{2}Nk, \\ c_{\rm V} &= \frac{f}{2}N_{\rm A}k. \end{align*}\]

The uppercase \(C_{\rm V}\) denotes the heat capacity for a general amount, where the lowercase \(c_{\rm V}\) is per mole.

Table 8.1 Molar Heat Capacities for Selected Gases at \(15^\circ C\) and \(1\ {\rm atm}\)

Gas	\(\mathbf{c_{\rm V} \mathbf{\rm (J/K)}}\)	\(\mathbf{c_{\rm V}/R}\)
\(\rm Ar\)	12.5	1.50
\(\rm He\)	12.5	1.50
\(\rm CO\)	20.7	2.49
\(\rm H_2\)	20.4	2.45
\(\rm HCl\)	21.4	2.57
\(\rm N_2\)	20.6	2.49
\(\rm NO\)	20.9	2.51
\(\rm O_2\)	21.1	2.54
\(\rm Cl_2\)	24.8	2.98
\(\rm CO_2\)	28.2	3.40
\(\rm CS_2\)	40.9	4.92
\(\rm H_2S\)	25.4	3.06
\(\rm N_2O\)	28.5	3.42
\(\rm SO_2\)	31.3	3.76

Table 8.1 shows the molar heat capacities for selected gases in terms of the heat capacity \(c_{\rm V}\) and a value normalized by the ideal gas constant \(R=N_{\rm A} k\).

There is no law where our three models (translational, rotation, and vibrational) must remain separate. Therefore, we should expect a lower limit of \(1.5\) for \(c_{\rm V}/R\), where an upper limit may be \({\sim}3.5\). The upper limit is less defined due to other assumptions in our approximations and the chosen temperature.

• For \(\rm He\) gas, we see good agreement for only translational kinetic energy.

• For \(\rm CO\) gas, there is good agreement for translational and rotational kinetic energy.

• For \(\rm CO_2\) gas, it approaches our estimate for all three sources of kinetic energy.

If we compared the gases at higher temperatures, then the vibrational mode can be more easily excited for a diatomic gas. In a polyatomic gas, it can be more complex where the number of “normal modes” increases with the number of masses in the system. As a result, the vibrational modes “turn on” at different temperatures.

Thermal model in a solid

The thermal molecular motion in a solid is limited to only the vibrational mode as the atoms from structures that prevent tranlations and rotations. How many degrees of freedom are in the system?

A 1-D harmoic oscillator has two degrees of freedom (1 from kinetic energy and another from the potential energy). For a 3-D oscillator, thre are six degrees of freedom and the molar heat capacity is \(6\left(\frac{1}{2}R\right) = 3R\).

The experimental value of molar heat capacity is almost exactly \(3R\) for Copper \((Cu)\) near room temperature.

Exercise 8.2

Consider the gases \(\rm HF\) and \(\rm Ne\) at a temperature of \(300\ {\rm K}\). Compare the average translational kinetic energy and total kinetic energy of the two types of molecules.

The \(\rm HF\) and \(\rm Ne\) have about the same molecular mass \((20\ \rm u)\), where \(1\ {\rm u} = 1.66054 \times 10^{-27}\ {\rm kg}.\)

• According to the equipartition theorem, the molecules’ translational kinetic energy are the same, \(\frac{3}{2}RT\) per mole.

• The monatomic \(\rm Ne\) has no rotational degrees of freedom, so its total kinetic energy is equal to the translational kinetic energy.

• The diatomic \(\rm HF\) has two rotational degrees of freedom, where its total kinetic energy is \(\frac{5}{2}RT\) per mole.

8.4. Maxwell Speed Distribution

The general form of the Maxwell velocity distribution is given as

\[\begin{align*} f(\vec{v})\ d^3\vec{v} = C e^{-\frac{1}{2}\beta m v^2}\ d^3\vec{v}, \end{align*}\]

where \(C = {C^\prime}^3 = \left(\frac{\beta m}{2\pi}\right)^{3/2}\).

The distribution \(f(\vec{v})\) is a function of the speed \(v\) in the exponent and not the velocity \(\vec{v}\), but it is still a velocity distribution due to the phase space volume element \(d^3\vec{v}\). We can turn this velocity distribution into a speed distribution \(F(v)\) using the definition

\[\begin{align*} F(v)\ dv =& \text{ probability of finding a particle } \\ & \text{ with speed between } v\ \text{and}\ v + dv. \end{align*}\]

Consider the analogous problem in 3-D position space \((x,\ y,\ z)\). Some distribution of particles exist, where a particle can be located with \((x,\ y,\ z)\) with a distance \(r = \sqrt{x^2+ y^2 + z^2}\) from the origin and has a position vector \(\vec{r}\) measured relative to the origin. Then

\[\begin{align*} f(x,\ y,\ z)\ d^3\vec{r} = & \text{ probability of finding a particle} \\ & \text{ between }\vec{r}\ \text{and}\ \vec{r} + d^3\vec{r}, \end{align*}\]

with \(d^3\vec{r} = dx\ dy\ dz\). To shift to the scalar radial distribution we introduce the definition

\[\begin{align*} F(r)dr = & \text{ probability of finding a particle} \\ & \text{ between }r\ \text{and}\ r + dr. \end{align*}\]

The space between \(r\) and \(r+dr\) is a spherical shell, and thus, we must integrate over that volume to transform to the radial distribution. These two distributions are related by the volume of spherical shell, or \(4\pi r^2\). We may write

(8.12)\[\begin{align} F(r)dr = f(x,\ y,\ z) 4\pi r^2\ dr. \end{align}\]

Returning to the problem of the speed distribution \(F(v)\) from the velocity distribution \(f(\vec{v})\). We need to integrate over a spherical shell in the velocity phase space, where we replace \(r\rightarrow v\) from the previous example. The desired speed distribution is

Maxwell speed distribution

(8.13)\[F(v)\ dv = 4\pi Ce^{-\frac{1}{2}\beta m v^2}v^2\ dv.\]

The Maxwell speed distribution as derived from purely classical considerations, where it gives a nonzero probability of finding a particle with a speed greater than \(c\). Therefore, it is only valid in the classical limit.

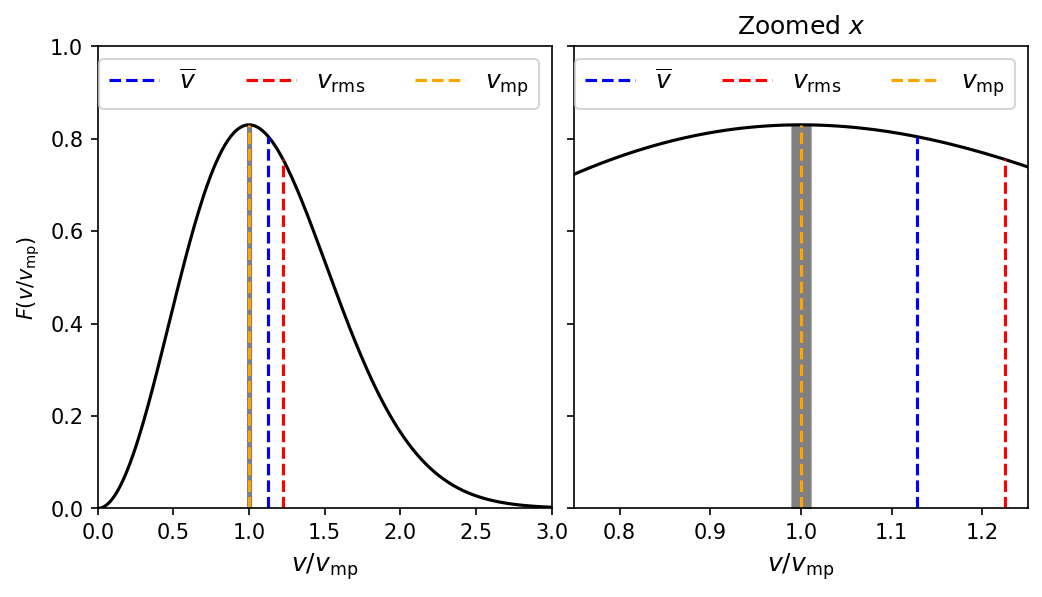
The assymetry of the distribution curve leads to an interesting result:

the most probable speed \(v_{\rm mp}\), the mean speed \(\bar{v}\), and the root-mean-square speed \(v_{\rm rms}\) are all slightly different from each other.

To find the most probable speed, we simply find maximum speed in the probabilty curve, or

(8.14)\[\begin{align} \frac{dF}{dv} &= 4\pi C \frac{d}{dv}\left[e^{-\frac{1}{2}\beta m v^2}v^2 \right], \\ &= 2ve^{-\frac{1}{2}\beta m v^2} - \left(\beta m v\right)v^2 e^{-\frac{1}{2}\beta m v^2}. \end{align}\]

Replacing \(v\rightarrow v_{\rm mp}\) to denote the most probable speed and setting the above result equal to zero, we can solve for \(v_{\rm mp}\):

Most probable speed \(v_{\rm mp}\)

(8.15)\[\begin{align} 2v_{\rm mp}e^{-\frac{1}{2}\beta m v_{\rm mp}^2} &= \left(\beta m v_{\rm mp}\right)v_{\rm mp}^2 e^{-\frac{1}{2}\beta m v_{\rm mp}^2}, \\ v_{\rm mp} &= \sqrt{\frac{2}{\beta m}} = \sqrt{\frac{2kT}{m}}. \end{align}\]

A particle moving at the most probable speed has a kinetic energy \(K_{\rm mp} = \frac{1}{2}mv_{\rm mp}^2 = kT\).

The mean speed is found by integrating (summing up) the probabilities for individual speeds, or

\[\begin{align*} \bar{v} = \int_0^\infty vF(v)\ dv = 4\pi C \int_0^\infty v^3e^{-\frac{1}{2}\beta m v^2}dv. \end{align*}\]

See a list of integrals containing exponential functions and using \((k=1,\ n=3,\ a=\beta m/2)\) to find

Mean speed \(\bar{v}\)

(8.16)\[\begin{split}\bar{v} &= 4\pi C \left(\frac{1}{2(\beta m/2)^2}\right) = 8\pi \left(\frac{\beta m}{2\pi}\right)^{3/2} \left(\frac{1}{(\beta m)^2}\right), \\ &= \frac{4}{\sqrt{2\pi}} \left(\frac{1}{\sqrt{\beta m}}\right), \\ &= \frac{2}{\sqrt{\pi}} \sqrt{\frac{2kT}{m}}, \\ &= \frac{2}{\sqrt{\pi}} v_{\rm mp}.\end{split}\]

We define the root-mean-square \(v_{\rm rms}\) to be \( v_{\rm rms} \equiv \left(\overline{v^2}\right)^{1/2}\). We cannot simply use the result for the mean speed \(\bar{v}\) directly. Instead, we need to find the mean using the probability function \(F(v)\), or

\[\begin{align*} \overline{v^2} = \int_0^\infty v^2F(v)\ dv = 4\pi C \int_0^\infty v^4e^{-\frac{1}{2}\beta m v^2}dv. \end{align*}\]

See a list of integrals containing exponential functions and using \((k=2,\ n=4,\ a=\beta m/2)\) to find

(8.17)\[\begin{align} \overline{v^2} &= 4\pi C \int_0^\infty v^4e^{-\frac{1}{2}\beta m v^2}dv = 4\pi C \left(\frac{3!!}{8a^2}\sqrt{\frac{\pi}{a}}\right), \\ &= 4\pi \left(\frac{\beta m}{2\pi}\right)^{3/2} \frac{3}{2(\beta m)^2} \sqrt{\frac{2\pi}{\beta m}}, \\ &= \frac{3(\beta m)^{3/2}}{(\beta m)^{5/2} } = \frac{3}{\beta m}, \\ &= \frac{3kT}{m}. \end{align}\]

Then

Root-mean-square speed \(v_{\rm rms}\)

(8.18)\[\begin{align} v_{\rm rms} = \left(\overline{v^2}\right)^{1/2} = \sqrt{\frac{3kT}{m}} = \sqrt{\frac{3}{2}}v_{\rm mp}. \end{align}\]

A particle moving with the mean squared speed has a kinetic energy

\[ \overline{K} = \frac{1}{2}m\overline{v^2} = \frac{1}{2}m \left(\frac{3kT}{m}\right) = \frac{3}{2}kT \]

in keeping with our basic law of kinetic theory.

The standard deviation of the molecular speeds \(\sigma_v\) is

(8.19)\[\begin{align} \sigma_v &= \left(\overline{v^2} - \bar{v}^2\right)^{1/2} = \left(\frac{3kT}{m} - \frac{8kT}{m\pi}\right)^{1/2}, \\ &= \left[\frac{(3\pi-8)kT}{m\pi}\right]^{1/2},\\ &= \left[3-\left(\frac{8}{\pi}\right)\right]^{1/2} \sqrt{\frac{kT}{m}}, \\ &= \left[\frac{3}{2}-\left(\frac{8}{2\pi}\right)\right]^{1/2} v_{\rm mp}. \end{align}\]

Exercise 8.3

Computre the mean molecular speed \(\bar{v}\) in hydrogen \(({\rm H_2})\) and radon \(({\rm Rn})\) gas, both at room temperature \(293\ {\rm K}\). Use the longest-lived radon isotope, which has a molar mass of \(222\ {\rm u}\). Compare the results.

The mean molecular speed is given by

\[ \bar{v} = \frac{2}{\sqrt{\pi}} \sqrt{\frac{2kT}{m}}, \]

which can be applied to each type of gas. The only difference between results will be due to the molar mass \(m\). The molar mass of \(\rm H_2\) is \(2.01568\ {\rm u}\), which is found by multiplying the mass of hydrogen by two. The conversion from atomic mass units \({\rm u}\) to \(\rm kg\) is \(1.660539 \times 10^{-27}\ {\rm kg/u}\). Let’s re-write the mean molecular speed so that all the physical constants are combined and so that we can use atomic mass units directly. This gives

(8.20)\[\begin{align} \bar{v} = \left(2\sqrt{\frac{2k}{\pi u}}\right)\sqrt{\frac{T\ \text{(in K)}}{m\ \text{(in u)}}} = 145.5081\sqrt{\frac{T}{m}}. \end{align}\]

Then, we compute the mean molecular speed for molecular hydrogen \(\rm H_2\) as

\[ \bar{v}_{\rm H_2} = 145.5081\sqrt{\frac{293}{2.01568}} = 1750\ {\rm m/s}.\]

The mean molecular speed for radon \({\rm Rn}\) can be calculated a mass ratio because the temperature is the same in both cases. From this method we find that the mean speed is:

\[ \bar{v}_{\rm Rn} = \sqrt{\frac{2.01568}{222}}\bar{v}_{\rm H_2} = 166\ {\rm m/s}.\]

The hydrogen molecule is \({\sim}10\times\) faster on average. That’s to be expected because the mass ratio \((m_{\rm Rn}/m_{\rm H_2}) \sim \sqrt{100} = 10.\)

import numpy as np
from scipy.constants import physical_constants 

def mean_molecular_speed(T,m):
    #T = absolute temperature in K
    #m = molar mass in u
    return (2/np.sqrt(np.pi))*np.sqrt((2*k*T)/(m*u))

k = physical_constants['Boltzmann constant'][0]
u = physical_constants['atomic mass constant'][0]
mean_speed_constant = 2/np.sqrt(np.pi)*np.sqrt(2*k/u)

T = 293 #room temperature in K
m_H2 = 2.01568 #molar mass in u
m_Rn = 222 #molar mass in u
mass_ratio = m_Rn/m_H2

v_H2 = np.round(mean_molecular_speed(T,m_H2),-1)
v_H2_constant = np.round(mean_speed_constant*np.sqrt(T/m_H2),-1)

print("----For hydrogen-----")
print("The mean molecular speed of molecular hydrogen (H_2) is %i m/s." % v_H2)
print("The mean molecular speed using our simplified equation is %i m/s." % v_H2_constant)

print("----For radon-----")
v_Rn = v_H2/np.sqrt(mass_ratio)
print("The mean molecular speed of radon gas (Rn) is %i m/s." % v_Rn)
print("The mass ratio (m_Rn/m_H2) is %i and the ratio of speeds (v_H2/v_Rn) is %1.1f." % (mass_ratio, np.sqrt(mass_ratio)))

----For hydrogen-----
The mean molecular speed of molecular hydrogen (H_2) is 1750 m/s.
The mean molecular speed using our simplified equation is 1750 m/s.
----For radon-----
The mean molecular speed of radon gas (Rn) is 166 m/s.
The mass ratio (m_Rn/m_H2) is 110 and the ratio of speeds (v_H2/v_Rn) is 10.5.

Exercise 8.4

What fraction of the molecules in an ideal gas in equilibrium has speeds with \(\pm1\%\) of the most probable speed \(v_{\rm mp}\)?

The Maxwell speed distribution function provides the probability of finding a particle within an interval of speeds. The fraction of molecules within the a given speed interval is equal to the integrated probability over the interval. Mathematically, this is expressed by the number of molecules at a particular speed \(N(v)\):

(8.21)\[\begin{align} P(\pm1\%) = \frac{N(1.01v_{\rm mp})-N(0.99v_{\rm mp})}{N} = \int_{0.99v_{\rm mp}}^{1.01v_{\rm mp}} F(v)dv. \end{align}\]

The indefinite integral introduces the error function, which is beyond the scope of this course. However, we can obtain an approximate solution by calculating \(F(v_{\rm mp})\) and multiplying by \(dv \approx \Delta v = 0.02v_{\rm mp}\). This solution works for a small window, where wider intervals are easily evaluated using numerical methods (e.g., Simpson’s rule).

Recall the most probable speed \(v_{\rm mp} = \sqrt{\frac{2}{\beta m}}\) and substitute to get

\[\begin{align*} F(v_{\rm mp}) &= 4\pi \left(\frac{\beta m}{2\pi}\right)^{3/2} v_{\rm mp}^2 e^{-\frac{1}{2}\beta m v_{\rm mp}^2}, \\ &= 4\pi \sqrt{\frac{\beta m}{2\pi}}\left(\frac{\beta m}{2\pi}\right) \left(\frac{2}{\beta m}\right) e^{-\frac{1}{2}\beta m \frac{2}{\beta m}}, \\ &= \frac{4}{e} \sqrt{\frac{\beta m}{2\pi}}. \end{align*}\]

Then applying our approximation

\[\begin{align*} P(\pm1\%) &= F(v_{\rm mp})(0.02v_{\rm mp}),\\ &= \frac{4}{e} \sqrt{\frac{\beta m}{2\pi}} (0.02) \sqrt{\frac{2}{\beta m}}, \\ &= \frac{4}{\sqrt{\pi}}(0.02 e^{-1}) \approx 0.017. \end{align*}\]

The python code plots the Maxwell speed distribution for an ideal gas using \(g=v/v_{\rm mp}\) for the \(x\)-axis coordinate, where the vertical lines denote the mean, root-mean-squared, and most probable speeds. It also numerically calculates (via Simpson’s rule) the proability and finds good agreement with our approximation (\(0.0166\)).

import numpy as np 
import matplotlib.pyplot as plt 
from scipy.integrate import simpson

def Maxwell_speed(g):
    #g = v/v_mp or v = g*v_mp
    return 4/np.sqrt(np.pi)*g**2*np.exp(-g**2)

v_rng = np.arange(0.99,1.01,0.0001)
prob = simpson(Maxwell_speed(v_rng),v_rng)
print("The fraction of molecules with speeds within 1 percent of v_mp is %1.4f." % prob)

fig = plt.figure(figsize=(8,4),dpi=150)
ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(122)
ax_list = [ax1,ax2]

g = np.arange(0, 3,0.01)
for i in range(0,2):
    ax = ax_list[i]
    ax.plot(g,Maxwell_speed(g),'k-',lw=1.5)
    ax.axvline(2/np.sqrt(np.pi),0,Maxwell_speed(2/np.sqrt(np.pi)),color='b',linestyle='--',label='$\\overline{v}$')
    ax.axvline(np.sqrt(1.5),0,Maxwell_speed(np.sqrt(1.5)),color='r',linestyle='--',label='$v_{\\rm rms}$')
    ax.axvline(1,0,Maxwell_speed(1),color='orange',linestyle='--',label='$v_{\\rm mp}$')
    ax.fill_between(v_rng,0,Maxwell_speed(v_rng),color='gray')

    ax.legend(loc='best',ncols=3,fontsize='large')
    
    ax.set_xlabel("$v/v_{\\rm mp}$",fontsize='large')
    ax.set_ylim(0.,1)

ax1.set_ylabel("$F(v/v_{\\rm mp})$")
ax1.set_xlim(0,3)
ax2.set_xlim(0.75,1.25)
ax2.set_title("Zoomed $x$")
ax2.set_yticklabels([])

fig.subplots_adjust(wspace=0.05);

The fraction of molecules with speeds within 1 percent of v_mp is 0.0166.

8.5. Classical and Quantum Statistics

The Maxwell speed distribution is only valid in the classical limit, which prohibits its use at exceptionally high temperatures (i.e., gas particle velocities near \(c\)). An ideal gas is dilute, which means that the gas molecules rarely interact or collide with one another due to their large (relative) separations. When collisions occur, they can be treated as totally elastic, and have no effect on the distributions and mean values.

When the density of matter is higher (i.e., solid or liquids), the assumption of noninteracting particles may no longer be valid. If molecules, atoms, or subatomic particles are closely packed together, the Pauli exclusion principle prevents two particles in identical quantum states from sharing the same s=pace. This limits the allowed energy states of any particle (fermion), which affects the distribution of energies for a system of particles.

8.5.1. Classical Distributions

Because energy levels are fundamental in quantum theory, we rewrite the Maxwell speed distribution in terms of energy rather than velcocity. For a monatomic gas, the energy is all translational kinetic energy. We can use the following relations

(8.22)\[\begin{align} E &= \frac{1}{2}mv^2, \\ dE &= mv dv, \\ dv &= \frac{dE}{\sqrt{2mE}}. \end{align}\]

Similar to our derivation of the Maxwell speed distribution (see Eq.(8.13)), we can transform \(F(v) \rightarrow F(E)\),

Maxwell-Boltzmann energy distribution

(8.23)\[\begin{align} F(v)\ dv &= 4\pi C e^{-\frac{1}{2}\beta mv^2}v^2\ dv, \\ &= 4\pi C e^{-\beta E}\left( \frac{2E}{m}\right) \frac{dE}{\sqrt{2mE}}, \\ &= \frac{8\pi C}{\sqrt{2m^3}} e^{-\beta E}\sqrt{E}\ dE. \end{align}\]

to get the Maxwell-Boltzmann energy distribution. The factor \(e^{-\beta E}\) is important because Boltzmann showed that this factor is a characteristic of any classical system, regardless of how quantities other than molecular speeds may affect the energy of a given state. We define the Maxwell-Boltzmann factor for classical systems as

Maxwell-Boltzmann factor

(8.24)\[\begin{align} F_{\rm MB} = Ae^{-\beta E}, \end{align}\]

where \(A\) is a normalization constant. The energy distribution for a classical system will then have the form

(8.25)\[\begin{align} n(E) = g(E)F_{\rm MB}, \end{align}\]

where \(n(E)\) is a distribution that represents the number of particles within a bin of energy from \(E\) to \(E+dE\).

The function \(g(E)\) is known as the density of states, or the number of states available per unit energy range. The density of states is an essential element in al distributions. The factor \(F_{\rm MB}\) is the relative probability that an energy state is occupied at a given temperature.

8.5.2. Quantum Distributions

In quantum theory, particles are described by wave functions. Indentical particles cannot be distinguished from one another if there is a significant overlap of their wave functions. It is this characteristic that makes quantum statistics different from classical stastics.

Suppose that we have a system of just two particles. Each particle has an equal probability (0.5) of existing in either of two energy states. If the particles are distinguishable (e.g., labeled A and B), then the possible configurations are

1. Both in state 1,

2. Either A or B in each state, but not together, or

3. Both in state 2.

These configurations can be illustrated using a probability table:

Table 8.2 Probability Table of Two Particles (A & B)

State 1	State 2
AB
A	B
B	A
	AB

Each of the four configurations are equally likely, where the probability of each is one-fourth (0.25). If the two particles are indistinguishable, then our probability table changes:

Table 8.3 Probability Table of Two Indistinguishable Particles

State 1	State 2
XX
X	X
	XX

Now there are only three equally likely configurations, where each have a probability of one-third (\({\sim}0.33\)).

Two kinds of quantum distributions are needed because some particles obey the Pauli exclusion principle and others do not.

• Particles that obey the Pauli exclusion princple have half-integers spins and are called fermions. Protons, neutrons, and electrons are examples of fermions.

• Particles with zero or integer spins do not obey the Pauli exclusion principle and are known as bosons. Photons and pions are examples of bosons.

Note

Atoms and molecules consisting of an even number of fermions must be bosons when considered as a whole, because their total spin will be zero or an integer. Conversely, atoms and molecules with an odd number of fermions are fermions.

The probability distribution of fermions are given by the Fermi-Dirac distribution:

Fermi-Dirac distribution

(8.26)\[\begin{align} n(E) &= g(E)F_{\rm FD},\ \qquad \text{where } \\ F_{\rm FD} &= \frac{1}{B_{\rm FD}\ e^{\beta E}+1}. \end{align}\]

Similarly the Bose-Einstein distribution is valid for bosons and is

Bose-Einstein distribution

(8.27)\[\begin{align} n(E) &= g(E)F_{\rm BE},\ \qquad \text{where } \\ F_{\rm BE} &= \frac{1}{B_{\rm BE}\ e^{\beta E}-1}. \end{align}\]

In each case \(B_i\) (\(B_{\rm FD}\) or \(B_{\rm BE}\)) represents a normalization factor, and \(g(E)\) is the density of states appropriate for a particular situation.

Note

The Fermi-Dirac and Bose-Einstein distributions look very similar, where they differ only by the normalization constant and by the sign attached to the \(1\) in the denominator.

Both the Fermi-Dirac and Bose-Einstein distributions reduce to the classical Maxwell-Boltzmann distribution when \(B_ie^{\beta E} \gg 1\) \((\text{recall }x\pm 1 \approx x\) for \(x\gg 1)\) and \(A = 1/B_i\). This means that the Maxwell-Boltzmann factor is much less than 1 (i.e., the probability that a particular energy state will be occupied is much less than 1).

Table 8.4 Classical and Quantum Distributions

Distributions	Properties	Examples	Function
Maxwell-Boltzmann	Identical, distinguishable	Ideal gases	\(F_{\rm MB} = Ae^{-\beta E}\)
Bose-Einstein	Identical, indistinguishable with integer spin	Liquid \(\rm ^4He\), photons	\(F_{\rm BE} = \frac{1}{B_{\rm BE}\ e^{\beta E}-1}\)
Fermi-Dirac	Identical, indistinguishable with half-integer spin	Electron gas	\(F_{\rm FD} = \frac{1}{B_{\rm FD}\ e^{\beta E}+1}\)

Exercise 8.5

Assume that the Maxwell-Boltmann distribution is valid in a gas of atomic hydrogen. What is the relative number of atoms in the ground state and first excited state at: \(293\ {\rm K}\), \(5000\ {\rm K}\), and \(10^6\ {\rm K}\)?

The relative number of atoms between the ground and first excited states can be determined by using the ratio of \(n(E_2)\) to \(n(E_1)\). Mathematically this is given as

(8.28)\[\begin{align} \frac{n(E_2)}{n(E_1)} &= \frac{g(E_2)}{g(E_1)} e^{-\beta(E_2-E1)}, \end{align}\]

where the density of states \(g(E_1) = 2\) for the ground state (spin up or down) and \(g(E_2) = 8\) for the first excited state (see Electron shells). For atomic hydrogen, \(E_2-E_1 = 10.2\ {\rm eV}\). Putting this together we can write

\[\begin{align*} \frac{n(E_2)}{n(E_1)} &= \frac{8}{2} e^{-\frac{10.2\ {\rm eV}}{kT}} = 4e^{-\frac{10.2\ {\rm eV}}{kT}}, \end{align*}\]

for a given temperature \(T\). Using the Boltzmann constant in \(\rm eV/K\), we can easily calculate the relative numbers as

\[\begin{align*} \frac{n(E_2)}{n(E_1)} &=& 4e^{-404} &\approx& 10^{-175}, \quad & \text{for }T = 293\ {\rm K}, \\ &=& 4e^{-23.7}\quad &\approx& 2\times 10^{-10}, \quad & \text{for }T = 5000\ {\rm K}, \\ &=& 4e^{-0.118} &\approx& 3.55, \quad & \text{for }T = 10^6\ {\rm K}. \end{align*}\]

At very high temperatures, the exponential factor approaches 1, so the result simply approaches the ratio of the density of states.

import numpy as np
from scipy.constants import physical_constants 

##For atomic hydrogen only

def energy(n):
    #n = energy level
    return -E_o/n**2 #energy in eV

def relative_states(n1,n2,T):
    #n2 = energy level 2; n2 > n1
    #n1 = energy level 1
    #T = temperature in K
    g2, g1 = 2*n2**2, 2*n1**2
    E2,E1 = energy(n2),energy(n1)
    return (g2/g1)*np.exp(-(E2-E1)/(k_eV*T))

k_eV = physical_constants['Boltzmann constant in eV/K'][0]
E_o = physical_constants['Rydberg constant times hc in eV'][0]

print("The relative number of atoms at 293 K is %1.2e." % relative_states(1,2,293))
print("The relative number of atoms at 293 K is %1.2e." % relative_states(1,2,5000))
print("The relative number of atoms at 293 K is %1.2f." % relative_states(1,2,1e6))

The relative number of atoms at 293 K is 1.21e-175.
The relative number of atoms at 293 K is 2.07e-10.
The relative number of atoms at 293 K is 3.55.

8.6. Fermi-Dirac Statistics

8.6.1. Introduction to Fermi-Dirac Theory

The Fermi-Dirac distribution helps us understand how collections of fermions behave, one of its most useful applications is for the problem of electrical conducion.

First, we consider the role of the factor \(B_{\rm FD}\). Like any other normalization factor, one could simply integrate over all allowed values of \(F_{\rm FD}\). The factor \(B_{\rm FD}\) is temperature dependent because of the parameter \(\beta\ (=1/kT)\). We express this temperature dependence as

(8.29)\[\begin{align} B_{\rm FD} = e^{-\beta E_{\rm F}}, \end{align}\]

where \(E_{\rm F}\) is the Fermi energy. Then we can rewrite the Fermi-Dirac distribution as

(8.30)\[\begin{align} F_{\rm FD} = \frac{1}{e^{\beta(E-E_{\rm F})}+1}. \end{align}\]

Notice what happens when \(E=E_{\rm F}\), \(F_{\rm FD} = 1/2\) (exactly). As a result, it is common to define the Fermi energy as the energy at which \(F_{\rm FD} = 1/2\).

Consider the temperature dependence of \(F_{\rm FD}\), where in the limit as \(T \rightarrow 0\):

(8.31)\[\begin{align} F_{\rm FD} &= \begin{cases} 1, & \text{for } E < E_{\rm F}, \\ 0, & \text{for } E > E_{\rm F}. \end{cases} \end{align}\]

• At \(T=0\), fermions occupy the lowest energy levels available to them. They cannot all be in the lowest level because that would violate the Pauli exclusion principle. Rather, fermions will fall all available energy levels up to a particular energy (i.e., the Fermi energy).

• Near \(T=0\), there is little chance thermal agitation will kick a fermion to an energy above \(E_{\rm F}\).

• As \(T\) increases from zero, more fermions jump to higher energy levels, resultying in a smooth transition rather than a sharp step.

It is sometimes useful to consider a Fermi temperature (\(T_{\rm F}\equiv E_{\rm F}/k)\).

• When \(T\ll T_{\rm F}\), the step function approximation is reasonably accurate.

• When \(T \gg T_{\rm F}\), \(F_{\rm FD}\) approaches a simple decaying exponential. Recall that at sufficiently high temperatures, we expect Maxwell-Boltzmann statistics to be reasonably accurate.

8.6.2. Classical Theory of Electrical Conduction

In 1900 Paul Drude developed a theory of electrical conduction to explain the observed conductivity of metals. His model assumed that the electrons existed as a gas of free particles. This is a fair assumption because (in a conductor) the outermost electron is weakly bound to the atom and easily stripped away, even by a very weak electric field.

In the Drude model, the mteal is treated as a lattice of positive ions with a electron gas that is free to flow through it. Just as in the case of ideal gases, electrons have a thermal kinetic energy proportional to temperature. The mean speed of an electron at room temperature is \({\sim}10^5\ {\rm m/s}\). But, the particle velocities in a gas are directed randomly. Therefore, ther will be no net flow of electrons unless an electric field is applied to the conductor.

When an electric field is applied, the negatively charged electrons flow in the direction opposite that of the field. According to Drude, their flow is severely restricted by collisions with the lattice ions. Using some basic assumptions from classical mechanics, Drude showed that the current in a conductor should be linearly proportional to the applied electric field. This is consistent with Ohm’s law.

Unfortunately, the numerical predictions of the theory were not as successful. One important prediction was that the electrical conductivity \(\sigma\) could be expressed as

(8.32)\[\begin{align} \sigma &= \frac{n}{m}e^2\tau, \end{align}\]

where \(n\) is the number density of conduction electrons, \(e\) is the electron charge, \(\tau\) is the average time between electron-ion collisions, and \(m\) is the electron mass. It is possible to measure \(n\) through the Hall effect.

The parameter \(\tau\) is not as easy to measure, but it can be estimated using transport theory. The best estimates of \(\tau\) produced a value of \(\sigma\) that is about one order of magnitude too small for most conductors. The Drude theory is incorrect in this prediction.

Mean free path

The mean time between collisions \(\tau\) should be simply the mean distance \(\ell\) traveled by an electron between collisions (i.e., the mean free path) divided by the mean speed \(\bar{v}\) of the electrons, \(\tau = \ell/\bar{v}\).

Then the electrical conductivity is expressed as

(8.33)\[\begin{align} \sigma &= \frac{n\ell}{m\bar{v}}e^2. \end{align}\]

Equation (8.16) shows that the mean speed is proportional to the square root of the absolute temperature. According to the Drude model, the conductivity is proportional to \(T^{-1/2}\). For most conductors the conductivity is nearly proportional to \(T^{-1}\), except at low temperatures. Drude’s classical model fails again.

There is the problem of calculating the electronic contribution to the heat capacity of a solid conductor. The heat capacity of a solid can be almost completely accounted for by considering the six degrees of freedom from lattice vibrations. This gives a molar heat capacity of \(c_{\rm V} = 3R\). According to the equipartion theorem, we need to add another \(3(\frac{1}{2}R)\) for the heat capacity of the electron gas, giving a total of \(\frac{9}{2}R\).

This is not consistent with experimental results. The electronic contribution to the heat capacity depends on temperature and is only \({\sim}0.02R\) per mole at room temperature.

8.6.3. Quantum Theory of Electrical Conduction

To obtain a better solution, we turn to quantum theory where it is necesary to understand how the electron energies are distributed in a conductor. We can use the Fermi-Dirac distribution, but we have a problem to find \(g(E)\), or the number of allowed states per unit energy.

What energy values should we use?

Let’s retain the “free electron” assumption of the Drude model and use the results of the 3-D infinite square-well potential because it corresponds physically to a cubic lattice of ions. The allowed energies are

(8.34)\[E = \frac{h^2}{8mL^2}\left(n_1^2 + n_2^2 + n_3^2 \right),\]

where \(L\) is the side-length of a cube and \(n_i\) are the integer quantum numbers.

Let’s first solve the problem at \(T=0\). The distribution at room temperature is very much like \(T=0\) because \(T_{\rm F}\) is high for conductive metals (e.g, \(T_{\rm F} = 80,000\ {\rm K}\) for \(\rm Cu\)).

The above allowed energies can be rewritten as

\[\begin{align*} E = r^2 E_c, \end{align*}\]

where \(r^2\ (= n_1^2 + n_2^2 + n_3^2)\) represents the “radius” of a sphere in phase space (also dimensionless) and \(E_c\) is just a constant, not the ground state energy.

We have defined \(r\) in this way to construct a geometric solution to the problem of deteriming \(g(E)\). Think of the \(n_i\) as the “coordianates” of a 3-D number space. The number of allowed states up to “radius” \(r\) (or up to energy \(E\)) is directly related to the spherical “volume” \(\frac{4}{3}\pi r^3\). The exact number of states up to radius \(r\) is

(8.35)\[\begin{align} N_r &= (2)\left(\frac{1}{8}\right) \left(\frac{4}{3}\pi r^3 \right). \end{align}\]

The extra factor of \(2\) comes from spin degeneracy (one spin up and spin down electron). The factor of \(1/8\) is necessary because we are restricted to positive quantum numbers (i.e., one octant of a 3-D number space).

The number of states \(N_r\) can be expressed as a function of \(E\):

(8.36)\[\begin{align} N_r &= \frac{1}{3} \pi r^3 = \frac{1}{3} \pi \left(\sqrt{\frac{E}{E_c}}\right)^3, \\ &= \frac{1}{3} \pi \left(\frac{E}{E_c}\right)^{3/2}. \end{align}\]

At \(T=0\), the Fermi energy is the energy of the highest occupied energy level. If there are a total of \(N\) electrons, then

\[ N = \frac{1}{3} \pi \left(\sqrt{\frac{E_{\rm F}}{E_c}}\right)^3. \]

We solve for \(E_{\rm F}\) to obtain

(8.37)\[\begin{split}E_{\rm F} &= \left(\frac{3N}{\pi}\right)^{2/3}E_c, \\ &= \frac{h^2}{8m}\left(\frac{3N}{\pi L^3}\right)^{2/3}.\end{split}\]

Equation (8.37) is useful because the ratio \(N/L^3\) is well knonw for most condutors, where it is the number density of conduction electrons at \(T=0\).

Exercise 8.6

Calculate the Fermi energy and temperature for copper.

Equation (8.37) can be used to compute the Fermi energy, provided the number density of conduction electrons is known. For copper, \(N/V = 8.47 \times 10^{28}\ {\rm m^{-3}}.\) We use \(V = L^3\) for a cube. This allows us to compute the Fermi energy as

\[\begin{align*} E_{\rm F} &= \frac{\left(6.626 \times 10^{-34}\ {\rm J\cdot s}\right)^2}{8\left(9.11 \times 10^{-31}\ {\rm kg}\right)} \left[ \frac{3\left( 8.47 \times 10^{28}\ {\rm m^{-3}} \right)}{\pi}\right]^{2/3}, \\ &= 1.13 \times 10^{-18}\ {\rm J} = 7.03\ {\rm eV}. \end{align*}\]

The Fermi temperature is

\[\begin{align*} T_{\rm F} = \frac{E_{\rm F}}{k} = \frac{1.13 \times 10^{-18}\ {\rm J}}{1.381 \times 10^{-23}\ {\rm J/K}} = 8.16 \times 10^4\ {\rm K}. \end{align*}\]

import numpy as np 
from scipy.constants import h, k, m_e, eV

def Fermi_energy(NV):
    #NV = number density of conduction electrons N/V
    return h**2/(8*m_e)*(3*NV/np.pi)**(2./3.)

def Fermi_temp(E_F):
    #E_F = Fermi energy
    return E_F/k

NV_Cu = 8.47e28 #number density of conduction electrons for Copper 
EF_Cu = Fermi_energy(NV_Cu)
TF_Cu = Fermi_temp(EF_Cu)

print("The Fermi energy for copper is %1.1e J or %1.2f eV." % (EF_Cu,EF_Cu/eV))
print("The Fermi temperature for copper is %1.2e K." % TF_Cu)

The Fermi energy for copper is 1.1e-18 J or 7.03 eV.
The Fermi temperature for copper is 8.16e+04 K.

The density of states can be calculated by differentiating \(N_r\) with respect to energy:

\[ g(E) = \frac{N_r}{dE} = \frac{\pi}{2}E_c^{-3/2}E^{1/2}. \]

This result can be expressed in terms of \(E_{\rm F}\) as

(8.38)\[\begin{align} g(E) &= \frac{\pi}{2} \left( E_{\rm F}^{-3/2} \frac{3N}{\pi}\right) E^{1/2}, \\ &= \frac{3}{2}N E_{\rm F}^{-3/2} E^{1/2}. \end{align}\]

Because we are considering \(T=0\), it is possible to use the step function form of the Fermi-Dirac factor. We have

(8.39)\[\begin{align} n(E) &= \begin{cases} g(E), &\text{for }E< E_{\rm F}, \\ 0, & \text{for } E>E_{\rm F}. \end{cases} \end{align}\]

With the distribution function \(n(E)\), the mean electron energy can be calculated as

(8.40)\[\begin{align} \overline{E} &= \frac{1}{N} \int_0^\infty n(E) E\ dE = \frac{1}{N} \int_0^{E_{\rm F}} g(E)E\ dE, \\ &= \frac{3}{2} \int_0^{E_{\rm F}} \left(\frac{E}{E_{\rm F}}\right)^{3/2} \ dE, \\ &= \frac{3}{2 E_{\rm F}^{3/2}} \int_0^{E_{\rm F}} E^{3/2}\ dE = \frac{3}{5} E_{\rm F}. \end{align}\]

We can now find the electronic contribution to the heat capacity of a conductor. Recall that the heat capacity at constant volue is \(C_{\rm V} = \partial U/\partial T\), where \(U\) is the internal energy. Using our result for \(\overline{E}\), we have

\[ U = N\overline{E} = \frac{3}{5}N E_{\rm F}. \]

The important question for determining the heat capacity is how \(U\) increases with temperature because the energy levels are filled up to \(E_{\rm F}\). We expect that only those electrons within about \(kT\) of \(E_{\rm F}\) will absorb thermal energy and jumpt to a higher state. The fraction of electrons capable of engaging in this thermal process is on the order of \(kT/E_{\rm F}\).

The exact number of electrons depends on the temperature because the shape of the curve for \(n(E)\) changes with temperature. In general, we can say

(8.41)\[\begin{align} U = \frac{3}{5}N E_{\rm F} + \alpha N \left(\frac{kT}{E_{\rm F}}\right) kT, \end{align}\]

where \(\alpha\) is a constant \(>1\) due to the shape of the distribution curve. Therefore the electronic contribution to the heat capacity is

\[\begin{align*} C_{\rm V} = \frac{\partial U}{\partial T} = 2\alpha N k^2 \frac{T}{E_{\rm F}}. \end{align*}\]

The molar heat capacity is

(8.42)\[\begin{align} c_{\rm V} = 2\alpha R \frac{T}{T_{\rm F}}, \end{align}\]

where \(R=N_{\rm A}k\) and \(E_{\rm F} = kT_{\rm F}\).

Arnold Sommerfeld used the correct distribution \(n(E)\) at room temperature and found \(\alpha = \pi^2/4\). With \(T_{\rm F} = 80,000\ {\rm K}\) for copper, we obtain \(c_{\rm V} = 0.02R\), which is also seen experimentally.

Fermi speed

To address the problem of electrical conductivity, we can replace the mean speed \(\bar{v}\) with what is called a Fermi speed \(u_{\rm F}\), defined from \(E_{\rm f} = \frac{1}{2}mu_{\rm F}^2\). We can justify this change because conduction electrons are the most loosely bound to their atoms. Therefore, these electrons must be at the highest energy level.

At room temperature, the highest energy level is close to the Fermi energy. This means that we should use

\[\begin{align*} u_{\rm F} &= \sqrt{\frac{2E_{\rm F}}{m}} \approx 1.6 \times 10^6\ {\rm m/s}, \end{align*}\]

for copper.

Unfortunately, this is an even higher speed than \(\bar{v}\). It turns out that there is a problem with the classical value Drude used for the mean free path \(\ell\). He assumed that the ions were so large and occupied so much space in a solid, the mean free path could be no more than \({\sim}0.1\ {\rm nm}\).

In quantum theory the ions are not hard spheres, and the electrons can be thought of as waves. Accounting for the wavelike property of electrons, the mean free path can be longer than Drude estimated. Einstein calculated the value of \(\ell\) to be \({\sim}40\ {\rm nm}\) for copper at room temperature. This gives a conductivity of

\[ \sigma = \frac{n\ell}{mu_{\rm F}} e^2 \approx 6 \times 10^7\ {\rm \Omega^{-1}\cdot m^{-1}}, \]

which is just right.

Finally, let’s consider the temperature dependence of the electrical conductivity. As the temperature of a conductor is increased, ionic vibrations become more severe. Thus electron-ion collsions will become more frequent, the mean free path will become smaller, and the conductivity will be reduced.

According to elementary transport theory, the mean free path is inversely proportional to the cross-sectional area of these ionic scatterers. Let’s assume that the ions are harmonic oscillators. The energy of a harmonic oscillator is proportional to the square of its vibration amplitude.

Therefore, the mean free path is inversely proportional to vibration energy (and temperature). We summarize this by

\[ \sigma \propto \ell \propto r^{-2} \propto U^{-1} \propto T^{-1}. \]

The electrical conductivity varies inversely with temperature. This is another success for quantum theory, where electrical conductivity is observed to vary inversely with temperature for most pure metals.

Exercise 8.7

Use the Fermi theory to compute the electronic contribution to the molar heat capacity of (a) copper and (b) silver at temperature \(T= 293\ {\rm K}\). Express the results as a function of the molar gas constant \(R\).

From the Fermi theory, we have

\[ c_{\rm V} = 2\alpha R \frac{T}{T_{\rm F}}, \]

where \(\alpha = \pi^2/4\).

(a) The Fermi temperature for copper is \(8.16 \times 10^4\ {\rm K}\) from the previous exercise. Substituting in the values gives

\[ c_{\rm V} = \frac{\pi^2\left(293\ {\rm K}\right)}{2\left(8.16\times 10^4\ {\rm K}\right)} R = 0.0177R \]

for copper, which rounds to \(0.02R\).

(b) The Fermi temperature for silver is \(6.38 \times 10^4\ {\rm K}\) (see Hyperphysics Table). Substituting in the values gives

\[ c_{\rm V} = \frac{\pi^2\left(293\ {\rm K}\right)}{2\left(6.38\times 10^4\ {\rm K}\right)} R = 0.0227R. \]

We see that the electronic contribution to the molar heat capacity is nearly the same for these two good conductors.

import numpy as np 

def heat_capacity_factor(T,TF):
    #T= given temp in K
    #TF = Fermi temp of conductor
    return np.pi**2/2*(T/TF)

T_room = 293 #room temperature in K
TF_Cu = 8.16e4 #Fermi temperature of copper in K
TF_Ag = 6.38e4 #Fermi temperature of silver in K 

cV_Cu = heat_capacity_factor(T_room,TF_Cu)
cV_Ag = heat_capacity_factor(T_room,TF_Ag)
print("The heat capacity for copper is %1.4f R." % cV_Cu)
print("The heat capacity for silver is %1.4f R." % cV_Ag)

The heat capacity for copper is 0.0177 R.
The heat capacity for silver is 0.0227 R.

8.7. Bose-Einstein Statistics

8.7.1. Blackbody Radiation

Recall the definition of an ideal blackboddy as a nearly perfect absorbing cavity that emits a spectrum of electromagnetic radiation (see Section 3.5). The problem is to find the intensity of the emitted radiation as a function of temperature and wavelength:

(8.43)\[\mathcal{I}(\lambda,T) = \frac{2\pi c^2 h}{\lambda^5} \frac{1}{e^{hc/(\lambda kT)}-1}. \]

In quantum theory, we begin with the assumption that the electromagnetic radiation is a collection of photons with energy \(hc/\lambda\). Photons are bosons with spin \(1\). We use the Bose-Einstein distribution to find how the photons are distributed by energy, and then convert the energy distribution into a function of wavlength via \(E= hc/\lambda.\)

The key to the problem is the density of states \(g(E)\). We model the photon gas just as we did for the electron gas: a collection of free particles within a 3-D infinite potential well. We cannot use Eq. (8.34) for the energy states because the photons are masseless.

We recast the solution to the particle-in-a-box problem in terms of mementum states rather than energy states. For a free particle of mass \(m\), the energy \(E=p^2/(2m)\). We rewrite Eq. (8.34) as

(8.44)\[\begin{align} p &= \sqrt{p_x^2 + p_y^2 + p_z^2}, \\ &= \frac{h}{2L}\sqrt{n_1^2 + n_2^2 + n_3^2}. \end{align}\]

The energy of a photon is \(E=pc\) so that

(8.45)\[\begin{align} E = \frac{hc}{2L}\sqrt{n_1^2 + n_2^2 + n_3^2}. \end{align}\]

Again by thinking of \(n_i\) as the coordinates of a number space and defining \(r^2 = n_1^2 + n_2^2 + n_3^2\), we find the number of allowed energy states within “radius” \(r\) is

\[ N_r = 2\left(\frac{1}{8}\right) \left( \frac{4}{3} \pi r^3\right). \]

This time the factor of \(2\) comes from the two possible photon polarizations. Also, the energy is proportional to \(r\) by

(8.46)\[\begin{align} E &= \frac{hc}{2L} r. \end{align}\]

We can then rewrite \(N_r\) in terms of \(E\) as

(8.47)\[\begin{align} N_r = \frac{1}{3} \pi r^3 = \frac{8\pi L^3}{3h^3 c^3} E^3. \end{align}\]

The density of states \(g(E)\) is

(8.48)\[\begin{align} g(E) = \frac{dN_r}{dE} = \frac{8\pi L^3}{h^3 c^3}E^2. \end{align}\]

The energy distribution is the product of the density of states and the a statistical factor. In this case, the Bose-Einstein factor:

(8.49)\[\begin{align} n(E) &= g(E)F_{\rm BE} = \frac{8\pi L^3}{h^3 c^3} E^2 \frac{1}{e^{E/(kT)}-1}. \end{align}\]

The normalization factor \(B_{\rm BE} = 1\) because we have a non-normalized collection of photons. As photons are absorbed and emitted by the walls of the cavity, the number of photons is not constant.

The next step is to convert from a number distribution to an energy density distribution \(u(E)\). Instead of number density \(N/V\), we use a factor \(E/L^3\) (energy per unit volume) as a multiplicative factor:

\[\begin{align*} u(E) = n(E)\frac{E}{L^3} = \frac{8\pi}{h^3 c^3}E^3 \frac{1}{e^{E/(kT)}-1}. \end{align*}\]

For all photons between \(E\) and \(E+dE\),

(8.50)\[\begin{align} u(E)\ dE = \frac{8\pi}{h^3 c^3} \frac{E^3\ dE}{e^{E/(kT)}-1}. \end{align}\]

Using \(E=hc/\lambda\) and \(|dE| = \left(hc/\lambda^2\right) d\lambda\)., we find

(8.51)\[\begin{align} u(\lambda, T)d\lambda = \frac{8\pi hc}{\lambda^5} \frac{ dE}{e^{E/(kT)}-1}. \end{align}\]

In the SI system, multiplying by a factor \(c/4\) is required to change energy density \(u(\lambda, T)\) to a spectral density \(\mathcal{I}(\lambda, T)\), or Eq. (8.43).

A few notes:

• Planck did not use the Bose-Einstein distribution to derive his radiation law. However, it shows the power of the statistical approach.

• This problem was first solved by Satyendra Nath Bose in 1924 before the concept of spin in quantum theory.

• Einstein’s name was added because he helped Bose publish his work in the West and later applied the distribution to other problems.

8.7.2. Liquid Helium

Helium has the lowest boiling point of any element (\(4.2\ {\rm K}\) at \(1\ {\rm atm}\)) and has no solid phase at normal pressures. In 1924 Kamerlingh Onnes, along with J. Boks, measured the density of liquid helium as a function of temperature, which shows that the density decreases for \(T>2.17\ {\rm K}\). A similar phenomenon occurs for the specific heat of liquid helium, as shown by Willem Keesom and Klaus Clusius in 1932 (see the orignal paper).

The python script below uses the data from Keesom & Clusius (1932) to demonstrate the changes in specific heat of liquid helium with temperature.

import numpy as np
import matplotlib.pyplot as plt 
from scipy.optimize import curve_fit 

def Bose_Einstein(T,A,b,c):
    return 1./(A*np.exp(b/(T+c))-1)

def Maxwell_Boltzmann(T,A,b,c):
    return A*np.exp(-b/(T+c))

#Data from Keesom and Clusius (1932); Specific heat in cal/(K g) and Temperature in K
#https://dwc.knaw.nl/DL/publications/PU00016277.pdf
Temp_Apr21 = np.array([1.315,1.33,1.593,1.98,2.126,2.089,2.113,2.125,2.134,2.147,2.16,2.172,2.184,2.205,2.23,2.257,2.282,2.305,2.33,2.356,2.451,2.613,2.784,2.949])
Spec_Heat_Apr21 = np.array([0.18,0.144,0.434,0.968,1.828,1.559,1.642,1.717,1.8,1.821,2.065,2.251,2.802,1.535,0.832,0.694,0.588,0.596,0.576,0.544,0.551,0.539,0.552,0.607])
Temp_Apr28 = np.array([2.12,2.137,2.15,2.16,2.17,2.179,2.186,2.196,2.21,2.231,2.253,2.279])
Spec_Heat_Apr28 = np.array([1.74,1.854,1.958,2.077,2.242,2.442,2.742,1.549,1.003,0.901,0.756,0.693])

Spec_Heat = np.concatenate((Spec_Heat_Apr21,Spec_Heat_Apr28))
Temp = np.concatenate((Temp_Apr21,Temp_Apr28))
Spec_Heat = Spec_Heat[Temp.argsort()]
Temp = Temp[Temp.argsort()]

fs = 'large'

fig = plt.figure(figsize=(5,5),dpi=150)
ax = fig.add_subplot(111)

ax.plot(Temp_Apr21,Spec_Heat_Apr21,'r.',ms=8)
ax.plot(Temp_Apr28,Spec_Heat_Apr28,'b.',ms=8)

left_idx = np.where(Temp<2.2)[0]
popt, pcov = curve_fit(Bose_Einstein,Temp[left_idx],Spec_Heat[left_idx],maxfev=8000)
Temp_range = np.arange(1.3,2.21,0.01)
ax.plot(Temp_range,Bose_Einstein(Temp_range,*popt),'k-',lw=1.5)

right_idx = np.where(Temp>=2.2)[0]
popt, pcov = curve_fit(Maxwell_Boltzmann,Temp[right_idx],Spec_Heat[right_idx])
Temp_range = np.arange(2.22,3,0.01)
ax.plot(Temp_range,Maxwell_Boltzmann(Temp_range,*popt),'k-',lw=1.5)

ax.set_xlim(1.3,3)
ax.set_ylim(0,3)

ax.set_ylabel("$c_{\\rm V}$ [$\\rm cal/(K\cdot g)$]",fontsize=fs)
ax.set_xlabel("Temperature ($\\rm K$)",fontsize=fs);

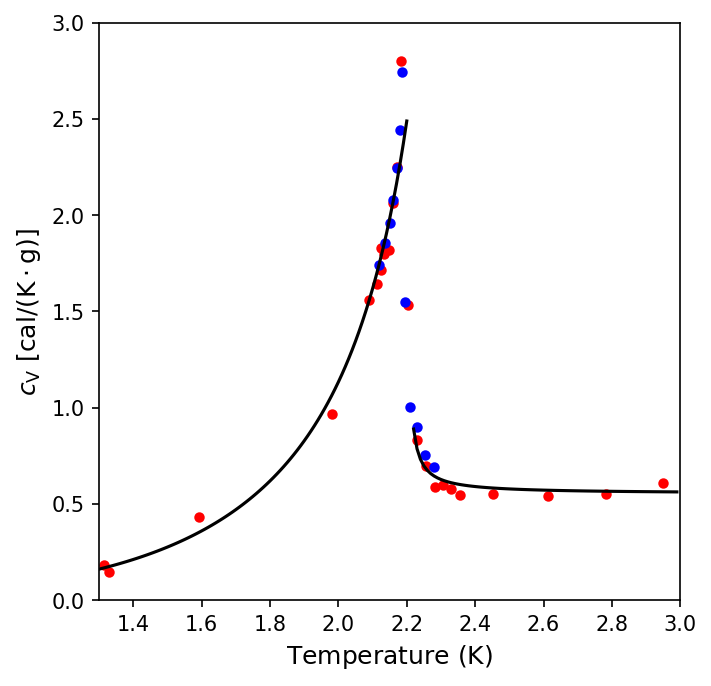
Something extraordinary is happening near \(2.17\ {\rm K}\), where this temperature is called the critical temperature \((T_c)\), transition temperature, or lambda point. The visual appearance of liquid helium is sufficient to demonstrate that something happens at the lambda point.

As the temperature is reduced from \(4.2\ {\rm K}\) toward the lambda point, the liquid boils vigorously. But at \(2.17\ {\rm K}\) the boiling suddenly stops, and the liquid becomes quite calm. At lower temepratures evaporation from the surface continues, but there is no further boiling. The transition across \(2.17\ {\rm K}\) is from the normal phase to the superfluid phase.

The word superfluid comes from a peculiar property of liquid helium below the lambda point. The flow rate of the liquid helium through a capillary tube as a function of temperature dramatically increases as the temperature is reduced. The superfluid has a lower viscosity than the normal fluid.

The viscosity can be so low that the superfluid helium forms what is called a creeping film and flows upwards (and over the vertical walls) of its container. If one tries to measure the viscosity of liquid helium (e.g., measuring the drag on a metal plate as it is passed over the surface of the liquid), the result is just about what one would get with a normal fluid, even at temperatures below the lambda point. There appears to be a contradiction between the experimental results for measuring viscosity and the capillary flow experiment.

Fritz London provided a theory, which claimed that the liquid helium below the lambda point is part superfluid and part normal. The superfluid component increases as the temperature is reduced from the lambda point. The fraction \(F\) of helium atoms in the superfluid follows fairly closely the relation

(8.52)\[\begin{align} F = 1 - \left( \frac{T}{T_c}\right)^{3/2}. \end{align}\]

The two-fluid model can explain our viscosity paradox, if we assume tha only the superfluid part participates in capillary flow and that enough normal fluid is always present to retard the motion of a metal plate dragged across its surface.

With two protons, two neutrons, and two electrons, the helium atom is a boson and therefore subject to Bose-Einstein statistics. Bosons are not subject to the Pauli exclusion principle, where there is no limit to the number that may occupy the same quantum state.

Bose-Einstein condensation

Superfluid helium is called a Bose-Einstein condensation into a single state, in this case the superfluid state. All the particles in a Bose-Einstein condensate are in the same quantum state, which is not forbidden for bosons. Note that \(\rm ^3He\) undergoes superfluidity, but in a different way where it is more like a fermion.

Bose-Einstein statistics can be used to estimate \(T_c\) for the superfluid phase of \(\rm ^4He\). Since bosons don’t follow the Pauli exclusion principle, their density of states is less by a factor of 2 (i.e., no need to account for spin pairing). As a result, we find

(8.53)\[\begin{align} g_{\rm BE}(E) = \frac{2\pi V}{h^3}\sqrt{8m^3 E}, \end{align}\]

with \(V\equiv L^3\) and \(m\) is the mass of the helium atom. The number distribution \(n(E)\) is

(8.54)\[\begin{align} n(E) &= g_{\rm BE}F_{\rm BE}, \\ &= \left(\frac{2\pi V}{h^3}\right) \frac{\sqrt{8m^3 E}}{B_{\rm BE}e^{E/(kT)}-1}. \end{align}\]

In a collection of \(N\) helium atoms, the normalization condition is

(8.55)\[\begin{align} N &= \int_0^\infty n(E)\ dE,\\ &=\left(\frac{2\pi V}{h^3}\right)\left(2m \right)^{3/2} \int_0^\infty\frac{\sqrt{ E}}{B_{\rm BE}e^{E/(kT)}-1}\ dE. \end{align}\]

Using \(u=E/(KT)\), this reduces to

(8.56)\[N = \left(\frac{2\pi V}{h^3}\right)\left(2m KT \right)^{3/2} \int_0^\infty\frac{\sqrt{ u}}{B_{\rm BE}e^u-1}\ du.\]

Definite Integral of the Type \(\int_0^\infty \frac{u^{n-1}}{e^u-1}\ du\)

Two special mathematical functions (the gamma and Riemann zeta functions) are needed to evaluate definite integrals from \(0\) to \(\infty\) with \(u^{n-1}\) in the numerator and \(e^u -1\) in the denominator. A handbook of integrals (see Gradshteyn & Ryzhik) will give the result

(8.57)\[\begin{align} \int_0^{\infty} \frac{u^{n-1}}{e^u-1}\ du = \Gamma(n)\zeta(n). \end{align}\]

In many cases in physics the gamma functions will have integer arguments, where we can evaluate them using the identity

(8.58)\[\begin{align} \textbf{Gamma function} \qquad & \Gamma(n) = (n-1)! = (n-1)(n-2)(n-3)\ldots(1). \end{align}\]

When \(n\) is not an integer, we can use the recursion formula

(8.59)\[\begin{align} \Gamma(n+1) = n\Gamma(n), \end{align}\]

with tabulated values of the gamma function, or scipy.special.gamma. There are some closed form solution for non-integer arguments, where \(\Gamma(1.5) = \sqrt{\pi}/2\).

Similar to the gamma function, we can use approporiate tables or scipy.special.zeta to obtain values for the Riemann zeta function \(\zeta(n)\). However it is helpful to know that the zeta function has some closed form solutions. For example,

(8.60)\[\begin{align} \zeta(2) &= \frac{\pi^2}{6}, \zeta(4) &= \frac{\pi^4}{90}. \end{align}\]

One integral of this form

\[\begin{align*} \int_0^\infty \frac{u^3}{e^u - 1}\ du \end{align*}\]

can be solved using \(n-1=3\) (or \(n=4\)) to get

\[\begin{align*} \int_0^\infty \frac{u^3}{e^u - 1}\ du = \Gamma(4)\zeta(4) = 3! \left(\frac{\pi^4}{90}\right) = \frac{\pi^4}{15}. \end{align*}\]

We do not know the value of \(B_{\rm BE}\), but we can proceed using the mininum allowed value \(B_{\rm BE} = 1\). To solve Eq. (8.56), we can re-write the integral to get gamma and Riemann zeta functions with \(n-1 = \frac{1}{2}\), or \(n=\frac{3}{2}\). Although \(\Gamma \left(\frac{3}{2}\right)\) has a closed-form solution, we resort to a numerical approximation for \(\zeta \left(\frac{3}{2}\right)\) or simply using the special function from scipy.

from scipy.special import gamma,zeta 

BE_integral = gamma(1.5)*zeta(1.5)

print("The integral for the Bose-Einstein distribution is approx %1.4f." % BE_integral)

The integral for the Bose-Einstein distribution is approx 2.3152.

Due to our assumption that \(B_{\rm BE} = 1\), this results in our determination of the maximum \(N\), which is

(8.61)\[\begin{align} N \leq \left(\frac{2\pi V}{h^3}\right)\left(2m KT \right)^{3/2} \left(2.3152 \right). \end{align}\]

We can rearrange the above expression to determine the minimum temperature as

(8.62)\[\begin{align} T \geq \frac{h^2}{2 mk}\left( \frac{N}{2\pi V (2.3152)}\right)^{2/3}. \end{align}\]

Using the number density of liquid helium in the normal state \((2.11 \times 10^{28}\ {\rm m^{-3}})\), we can find the minimum temperature for the normal state as

(8.63)\[\begin{align} T \geq 3.06\ {\rm K}. \end{align}\]

import numpy as np 
from scipy.special import gamma,zeta 
from scipy.constants import h,k, physical_constants 

m_He = 4.002603*physical_constants['atomic mass constant'][0] #mass of a helium atom (in kg)
NV_He = 2.11e28 #number density of liquid helium (in m^-3)

T_min = h**2/(2*m_He*k)*(NV_He/(2*np.pi*gamma(1.5)*zeta(1.5)))**(2./3.)

print("The minimum temperature for the normal state of liquid helium is %1.3f K." % T_min)

The minimum temperature for the normal state of liquid helium is 3.065 K.

The value \(3.06\ {\rm K}\) is an estimate of \(T_c\), where there is a condensation into the superfluid state at lower temperatures. Our result is a bit off, because we used a density of states derived for a noninteracting gas rather than a liquid. Calculation using a density of staes constructed specifically for a liquid produce even better results. We came tihin one kelvin of the correct value of \(T_c\), which isn’t that bad.

Exercise 8.8

For a gas of \(N_2\) at \(293\ {\rm K}\) and \(1\ {\rm atm}\), calculate the Maxwell-Boltzmann constant \(A\). Show that Bose-Einstein statistics can be replaced by Maxwell-Boltzmann statistics in this case.

Starting with the density of states for a boson gas:

\[ g(E) = \frac{2\pi V}{h^3}\sqrt{8m^3 E}\]

and the Maxwell-Boltzmann factor \((F_{\rm MB} = Ae^{-E/(kT)})\), we can determine the distribution \(n(E) = g(E)F_{\rm MB}\). The normalization comes from the integral to determine \(N\), or

\[\begin{align*} N = \int_0^\infty n(E)\ dE = \frac{2\pi V}{h^3} \left(2m \right)^{3/2} A \int_0^\infty E^{1/2} e^{-E/(kT)}\ dE. \end{align*}\]

Using an integral table with exponential functions, we use the relation

\[ \int_0^\infty u^n e^{-au}\ du = \Gamma(n+1)a^{-(n+1)} \]

to get

\[\begin{align*} N &= \frac{2\pi V}{h^3} \left(2m \right)^{3/2} A \Gamma\left(\frac{3}{2}\right) (kT)^{3/2}, \\ &= \frac{2\pi V}{h^3} \left(2m \right)^{3/2} A \frac{\sqrt{\pi}}{2} (kT)^{3/2}, \\ &= \frac{ V}{h^3} \left(2\pi mkT \right)^{3/2} A. \end{align*}\]

Solving for \(A\) gives

\[\begin{align*} A = \frac{h^3 N}{V} \left(2\pi mkT \right)^{-3/2}. \end{align*}\]

Under normal conditions (i.e., room temperature and pressure), the number density of nitrogen gas \(N/V = 2.5 \times 10^{25}\ {\rm m^{-3}}\). The molecular mass of \(N_2\) is \(28.02\ {\rm u}\). Substituting for the remaining physical constants, we find

\[\begin{align*} A &= (6.626 \times 10^{-34}\ {\rm J\cdot s})^3 (2.5\times 10^{25}\ {\rm m^{-3}}) (2\pi (4.64 \times 10^{-26}\ {\rm kg})(1.38 \times 10^{-23}\ {\rm J/K})(293\ \rm K))^{-3/2}, \\ &= 1.8 \times 10^{-7}. \end{align*}\]

Because this is much less than unity \((A\ll 1)\), the use of Maxwell-Boltzmann statistics is justified.

import numpy as np
from scipy.constants import h,k,physical_constants 

m_N2 = 28.02*physical_constants['atomic mass constant'][0] #mass of modecular Nitrogen (in kg)
print(m_N2)
NV_N2 = 2.5e25 #number density of N_2 (in m^-3)

T_room = 293 #room temp in K

A = h**3*NV_N2*(2*np.pi*m_N2*k*T_room)**(-3/2)

print("The normalization constant for N_2 as using the Maxwell-Boltzmann factor is %1.2e." % A)

4.6528304646132e-26
The normalization constant for N_2 as using the Maxwell-Boltzmann factor is 1.79e-07.

8.7.3. Symmetry of Boson Wave Functions

The properties of boson and fermion wave functions can be examined if we consider a system of two identical particles labeled “1” and “2”. For now the particles can be either bosons or fermions. The wave function that describes the two particles is \(\Psi(1,2)\). Because the two particles are identical, the probability density does not depend on their order:

\[ |\Psi(1,2)|^2 = |\Psi(2,1)|^2, \]

where solutions of this equation are

\[ \Psi(1,2) = \pm \Psi(2,1).\]

Symmetric and antisymmetric wave functions

• For \(\Psi(1,2) = \Psi(2,1)\), the wave functions are symmetric, where this will describe bosons.

• For \(\Psi(1,2) = -\Psi(2,1)\), the wave functions are antisymmetric, where this will describe fermions.

In a system of two noninteracting particles, the overall wave function can be expressed as a product of two individual wave functions (i.e., \(\Psi(1,2) = \psi(1)\psi(2)\)).

Suppose that the two particles are in different states, labeled \(a\) and \(b\). The net wave function for this system is a linear combination of the two possible combinations fo the particles in states \(a\) and \(b\). The symmetric wave function \(\Psi_{\rm S}\) and antisymmetric wavefunction \(\Psi_{\rm A}\) are written as:

(8.64)\[\begin{align} \Psi_{\rm S} &= \frac{1}{\sqrt{2}}\left[\psi_a(1)\psi_b(2) + \psi_a(2)\psi_b(1) \right] \qquad \text{and} \\ \Psi_{\rm A} &= \frac{1}{\sqrt{2}}\left[\psi_a(1)\psi_b(2) - \psi_a(2)\psi_b(1) \right], \end{align}\]

where in each case the factor \(1/\sqrt{2}\) is for normalization.

One imediate result is that the Pauli Exclusion Principle is justified. Suppose particles \(1\) and \(2\) are fermions in the same state. Then \(a=b\), and the antisymmetric wave function \(\Psi_{\rm A} = 0\), which is consistent with the principle that two fermions can’t occupy the same quantum state.

Bosons are governed by the symmetric wave function \(\Psi_{\rm S}\). If two bosons are in the same state, then the wave function becomes

\[\begin{align*} \Psi_{\rm S} &= \frac{1}{\sqrt{2}}\left[\psi_a(1)\psi_a(2) + \psi_a(2)\psi_a(1) \right], \\ &= \frac{2}{\sqrt{2}}\psi_a(1)\psi_a(2) \end{align*}\]

and the probability density for this state is

(8.65)\[\begin{align} \Psi_{\rm S}^*\Psi_{\rm S} &= \left(\frac{2}{\sqrt{2}}\right)^2 \left[\psi_a^*(1)\psi_a^*(2) \psi_a(1)\psi_a(2)\right], \\ &= 2 \left[\psi_a^*(1)\psi_a^*(2) \psi_a(1)\psi_a(2)\right]. \end{align}\]

Thus, two bosons have a nonzero probability of occupying the same state. If the conditions for Bose-Einstein condensation to occur, then it is likely to happen.

8.7.4. Bose-Einstein Condensation in Gases

For years physicists attempted to demonstrate Bose-Einstein condensation in gases. They were hampered, by the strong Coulomb interactions among the gas particles. This prevented them from obtaining the low temperatures and high densities needed to produce the condensate.

In 1995, a group led by Eric Cornell and Carl Wieman achieved success. Forming a Bose-Einstein condensate from a gas requires extremely low temperatures, which was possible through a two-step process.

1. They used laser cooling to cool their gas of \(\rm ^{87}Rb\) atoms to \({\sim}1\ {\rm mK}\).

2. They used a magnetic trap to cool the gas to a temperature of \({\sim}20\ {\rm nK}\) \((2 \times 10^{-8}\ {\rm K})\).

In their magnetic trap, the researchers varied the magnetic field at radio frequencies to drive away the atoms with higher speeds. What remained was an extremely cold, dense cloud. At temperatures \({\sim}170\ {\rm nK}\), the rubidium cloud passed through a transition from a gas with a normal, broad velocity distribution to an extremely narrow distribution. The fraction of atoms in teh condensed state increased as the temperature was lowered, just as in a super fluid.

In 1995, a group led by Wolfgang Ketterle confirmed Bose-Einstein condensation, but in sodium gas. For sodium, the transition to the condensed state was observed at \(2\ {\rm \mu K}\) (warm compared to \(20\ {\rm nK}\)).

Some physicists are exploring the possible applications of the Bose-Einstein condensation through an atom laser, which uses a collection of atoms in a Bose-Einstein condensate and emits them as a coherent beam.

Note that this beam of particles differs from the standard optical laser. The atom beam is much slower, because these relatively heavy particles are not accelerated anywhere near the speed of light. Other important differences are that new atoms cannot be created the way photons are created in an optical laser (limiting output) and the atoms in the beam interact with each other. The interaction makes the beam less focused and collimated when compared to an optical laser.

It is unlikely that atom lasers will replace optical lasers for retail scanners, CD/DVD readers, or surgery. They are used in atomic clocks and other precision measurements, as well as thin film deposition. The atom laser can be used to deposit a layer of atoms on a surface, and lithography, in which the beam etches the surface.