11. Nuclear Physics#
Ernest Rutherford has been called the “Father of the Nucleus.” He proposed a model of atomic structure that placed the heavy, positively charged nucleus at the center and the much ligher electrons at the periphery.
Around 1900, early investigators found that radioactive emissions from atoms comprised three types: \(\alpha\) (alpha), \(\beta\) (beta), and \(\gamma\) (gamma).
\(\alpha\) radiation is the least penetrating, where it can be stopped by a piece of paper. Early experiments established that \(\alpha\) rays were doubly charged positive particles.
\(\beta\) rays are more penetrating, where they are common and appearing in the emissions of many nuclei. Early experiments established that \(\beta\) rays were probably electrons.
\(\gamma\) radiation is the most penetrating, where it can pass through the human hand. Early experiments established that \(\gamma\) rays were electrically neutral.
Rutherford proved (in a series of experiments) that \(\alpha\) particles were the nuclei of helium atoms.
11.1. Discovery of the Neutron#
The composition of the nucleus was not determeined until 20 years after Rutherford proposed an atomic structure with the massive nucleus at the center (in 1912). Rutherford and others thought that a neutral particle might exist, but the existence of neutrons were not proven experimentally until 1932. James Chadwick found the first neutral particles using one of the first particle accelerators.
In the early 1900s, it was assumed that the nucleus was composed of both protons and electrons. There are several reason why electrons cannot exisit within the nucleus.
Nuclear size: To confine an electron in a space as small as a nucleus, the uncertainty principle puts a lower limit on its kinetic energy that is much larger than any kinetic energy observed fro an electron emitted from nuclei.
Nuclear spin: Protons and electrons have spin \(1/2\). If a dueteron (mass number \(A=2\); atomic number \(Z=1\)) consists of protons and electrons, the deuteron must contain \(2\) protons and \(1\) electron. However, \(3\) fermions must have a half-integral spin, whereas the nuclear spin of the deuteron has been measured to be 1.
Nuclear magnetic moment: The magnetic moment of an electron is over \(1000\times\) larger than that of a proton. However, the measured nuclear magnetic moment is comparable to the proton magnetic moment. In the proton and electron model, the nuclear magnetic moment would be on the same order as that of the electron.
It is difficult to understand how an electron can exist within the nucleus.
Exercise 11.1
What is the minimum kinetic energy of a proton in a medium-sized nucleus having a diameter of \(8\ {\rm fm}\) (\(1\ {\rm fm} = 10^{-15}\ {\rm m}\))?
Using the Heisenberg uncertainty principle, we can find the uncertainty in the momentum \(\Delta p\). We also use the value \(\hbar = 6.582 \times 10^{-16}\ {\rm eV\cdot s}\) so that the final energy can easily be written in units of \(\rm MeV\). The minimum kinetic energy can be written in terms of momentum, where we can then determine whether corrections from Special Relativity are required. The uncertainty \(\Delta p\) is
The momentum \(p\) must be as large as \(\Delta p\), where we have for
This is only \({\sim}1%\) of the proton’s rest energy \((938\ {\rm MeV})\), which means that we can treat the problem nonrelativistically. The kinetic energy \(\left[p^2/(2m)\right]\) of a proton in this nucleus must be as large as
The above result \(0.0809\ {\rm MeV}\) is a reasonable experimental value and consistent for a neutron.
import numpy as np
from scipy.constants import c, physical_constants
neutron_mass = physical_constants['neutron mass energy equivalent in MeV'][0]
hbar = physical_constants['Planck constant in eV/Hz'][0]/(2*np.pi)
delta_x = 8e-15 #nucleus size in m
delta_p = hbar/(2*delta_x)
p_min = delta_p*c/1e6
print("The minimum change in momentum is %1.4f eV s/m." % delta_p )
print("The minimum momentum is %2.2f MeV." % p_min)
KE = p_min**2/(2*neutron_mass)
print("The minimum kinetic energy is %1.4f MeV." % KE)
The minimum change in momentum is 0.0411 eV s/m.
The minimum momentum is 12.33 MeV.
The minimum kinetic energy is 0.0809 MeV.
There is strong experimental and theoretical evidence that electrons are not bound within the nucleus. Although all this evidence was not available to Rutherford (in 1920), he proposed that a neutral particle might exist called the neutron. The discovery of the neutron was preceded by other experimental investigtions that demonstrated how the nucleus could change.
In 1930, Walther Bothe and Herbert Becker were using a radioactive polonium source that emitted \(\alpha\) particles. Bothe and Becker found that when \(\alpha\) particles bombarded Beryllium, a very penetrating radiation was produced.
Irene Curie and Frederic Joliot showed in 1932 that the radiation could even penetrate several centimeters of lead.
This radiation could not be charged particles, because charged particles (of the energies available) could not penetrate even a short distance through lead. It was assumed that photons were produced in the \(\alpha\) bombardment of beryllium. These photons are called \(\gamma\) rays when they emanate from the nucleus. \(\gamma\) rays produced in the nucleus have energies on the order of \(\rm MeV\), which is much larger than the \(\rm keV\) x-ray photons produced by atomic transitions.
Curie and Joliot found that when the radiation passed through paraffin (which contains hydrogen) that protons with energies up to \(5.7\ {\rm MeV}\) were ejected. The simplest assumption was that the (gamma) radiation scattered by the Compton process from the hydrogen nuclei and knocked the protons out of the paraffin. The hypothesis of Compton scattering requires \(\gamma\) ray energies of at least \(50\ {\rm MeV}\) to produce \(5.7\ {\rm MeV}\) protons.
In 1932, James Chadwick proposed that the new radiation produced by \(\alpha + \rm Be\) consisted of neutrons (a neutrally charged particle with the mass of a proton). The neutrons would pass through material rather easily because it has a very small electromagnetic interaction via its magnetic moment. the nuclear force is very short-range, and a neutron having \(\rm MeV\) energies may have only a \(10^{-6}\) probability of intercting with a nucleus. Chadwick correctly surmised that if neutrons were produced in the \(\alpha + \rm Be\) reaction, the neutrons could then collide elasitcally with the protons in paraffin and account for the \(5.7\ {\rm MeV}\) protons.
11.2. Nuclear Properties#
The primary consituents of nuclei are the proton and neutron, where the nuclear mass is roughly the sum of its constituent proton and neutron masses (the slight difference resulting from the binding energy of the nucleus). The nuclear charge is the number of protons (\(Z\)) times the magnitude of the electron charge \(e = 1.6\times 10^{-19}\ {\rm C}\).
The simplest form of hydrogen has a single proton for a nucelus. Deuterium (“heavy hydrogen”) has a neutron and a proton in its nucleus. Another isotope of hydrogen (tritium) has two neutrons and one proton. The neuclei of deuterium and tritium are called deuterons and tritons, respectively.
The atomic (and nuclear) mass number \(A\) is the total integral number of protons and neutrons in the nucleus. Atoms with the same \(Z\) (but different \(A\)) are called isotopes. Deuterium (\(A=2\)) and tritium (\(A=3\)) are both isotopes of regular hydrogen \((A=1)\). The atomic mass \(M\) is the mass of the entire atom (including electrons) measured with a mass spectrograph.
An atomic nucleus is designated by
Each nuclear species with a given \(Z\) and \(A\) is called a nuclide.
When we write the nuclidic symbol for the better known elements \(Z\) is often omitted.
The nuclidic symbol \(A\) is always shown and \(N\) is often omitted because \(A = Z+N\) (e.g., \(\rm ^{16}_{\ \ 8} O_8 \rightarrow\) \(\rm ^{16}O\)).
Nuclides with the same neutron number are called isotones (e.g., \(\rm ^{14}_{\ \ 6} C\), \(\rm ^{15}_{\ \ 7} N\), \(\rm ^{18}_{\ \ 8} O\), and \(\rm ^{17}_{\ \ 9} F\)).
Nuclides with the same value of \(A\) are called isobars (e.g., \(\rm ^{16}_{\ \ 6} C\), \(\rm ^{16}_{\ \ 7} N\), \(\rm ^{16}_{\ \ 8} O\), and \(\rm ^{16}_{\ \ 9} F\)).
The chemical properties of an atom are determined by its electron configuration. The chemical properties are essentially determined by \(Z\) because a neutral atom will have equal numbers of electrons and protons.
Atomic masses are measured in atomic mass units, which are designated by the symbol \(\rm u\). Atomic mass units are defined in terms of the mass of the isotope \(\rm ^{12}C\) whose atomic mass is defined to be exactly \(12\ \rm u\). The atomic mass unit works out to be
Both neutrons and protons are known collectively as nucleons and are constructed of other particles called quarks*. Neutrons are slightly more massive than protons.
11.2.1. Sizes and Shapes of Nuclei#
Rutherford concluded from the \(\alpha\) particle scattering experiments of his assistants Geiger and Marsden that the range of the nuclear force must be less than \({\sim}10^{-14}\ {\rm m}\), where deviations from Coulomb’s law at that distance could be inferred from their data.
Assume that nuclei are spheres of radius \(R\). Particles (i.e., electrons, protons, \(\alpha\), etc.) scatter when projected close to the nucleus. It is not immediately clear whether the maximum interaction distance refers to the nuclear size (matter radius) or the nuclear force that could extend beyond the nuclear matter (force radius). Electrons do not respond to the nuclear force but scatter from the electromagnetic field of the nucleus. Thus, electron scattering measures the nuclear charge raidus.
The nuclear force is the strongest of the known forces (nuclear, gravitational, electroweak) at short distances. The nuclear force is often called the strong force. Because neutrons interact only with the nuclear force, the scattering of neutrons determines the nuclear force radius. Through many measurements, physicsists have found that
The nuclear radius is approximated by a spherical charge distribution with
where \(r_o \approx 1.2\ {\rm fm}\) and measurements range from \(1-1.5\ {\rm fm}\); Note \(1\ {\rm fm} = 10^{-15}\ {\rm m}\). However, the term fermi is also used interchangeably with femtometer.
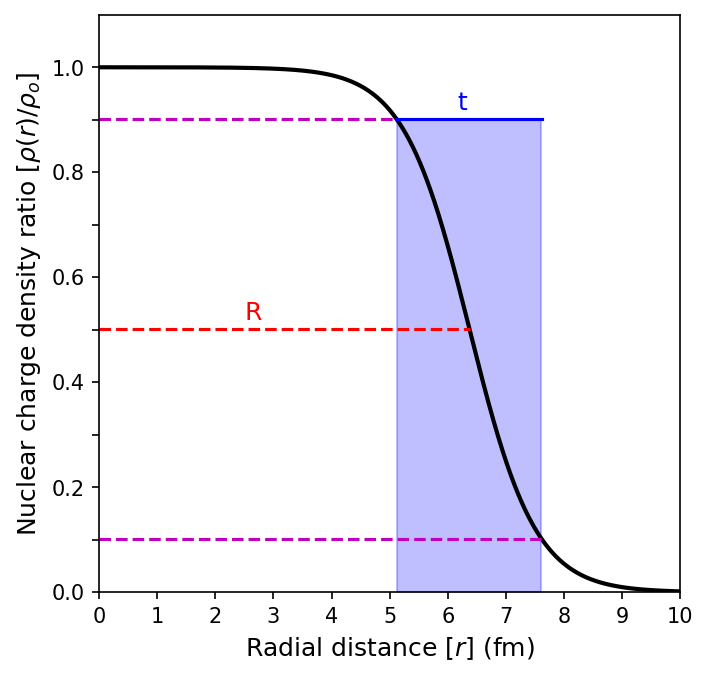
Robert Hofstadter and his colleagues (in the 1950s) performed the first precision electron-scattering measurements of the nuclear charge distribution using electron energies from \(100-500\ {\rm MeV}\). To probe the shape of most nuclei, we need a particle with a short wavelength. The de Broglie wavelength of a \(500\)-\(\rm MeV\) electron is \({\sim}2.5\ {\rm fm}\). These measurements are approximately described for all the lightest nuclei by the Fermi distribution for the nuclear charge density \(\rho(r)\) with the following form
The shape of the distribution shown below illustrates the distance \(R\) at which the nuclear density has dropped to \(50\%\) of its central value, and \(t = 4.4a\) is the surface thickness, measureed from \(90\%-10\%\) of the central density.
import numpy as np
import matplotlib.pyplot as plt
def nuclear_charge_density(r,R,a):
return 1./(1+np.exp((r-R)/a))
a_t = 2.5/4.4
r_o = 1.2 #nuclear radius (in fm)
A = 150
R = r_o*A**(1./3.) #distance where the nuclear density drops by 50% (in fm)
r = np.arange(0,10,0.001)
rho = nuclear_charge_density(r,R,a_t)
med_rho_idx = np.where(np.abs(rho-0.5)<1e-3)[0]
top_rho_idx = np.where(np.abs(rho-0.9)<1e-3)[0]
low_rho_idx = np.where(np.abs(rho-0.1)<1e-3)[0]
fig = plt.figure(figsize=(5,5),dpi=150)
ax = fig.add_subplot(111)
ax.plot(r,rho,'k-',lw=2)
ax.text(2.5,0.52,'$\\rm R$',fontsize='large',color='r')
ax.axhline(rho[med_rho_idx[0]],0,r[med_rho_idx[0]]/10,linestyle='--',color='r')
ax.axhline(rho[top_rho_idx[0]],0,r[top_rho_idx[0]]/10,linestyle='--',color='m')
ax.axhline(rho[low_rho_idx[0]],0,r[low_rho_idx[0]]/10,linestyle='--',color='m')
ax.text(6.15,0.92,'$\\rm t$',fontsize='large',color='b')
ax.axhline(rho[top_rho_idx[0]],r[top_rho_idx[0]]/10,r[low_rho_idx[0]]/10,linestyle='-',color='b')
x_fill = np.arange(r[top_rho_idx[0]],r[low_rho_idx[0]],0.01)
ax.fill_between(x_fill,0,rho[top_rho_idx[0]],color='b',alpha=0.25)
ax.set_ylim(0,1.1)
ax.set_xlim(0,10)
yticks = np.arange(0,1.1,0.1)
yticklabels = []
for f in range(0,11):
if f % 2 == 0:
yticklabels.append("%1.1f" % (0.1*f))
else:
yticklabels.append("")
ax.set_yticks(yticks)
ax.set_yticklabels(yticklabels)
ax.set_xticks(np.arange(0,11,1))
ax.set_ylabel("Nuclear charge density ratio $[\\rho(r)/\\rho_o]$",fontsize='large')
ax.set_xlabel("Radial distance $[r]$ (fm)",fontsize='large');
Exercise 11.2
What is the nuclear radius of \(\rm ^{40}Ca\)? What energy electrons and protons are required to probe the size of \(\rm ^{40}Ca\) if one wants to “see” at least half the radius?
Exercise 11.3
Find the radii of the \(\rm ^{238}U\) and \(\rm ^{4}He\) nuclei and then determine the ratio of those radii.
If we approximate the nuclear shape as a sphere, we have:
The nuclear mass density (mass/volume) can be determined from \((\rm A\ u)/V\) to be \(2.3\times 10^{17}\ {\rm kg/m^3}\). The nucleas is about \(10^{14}\) times denser than ordinary model.
The neutron and proton are fermions with spin quantum numbers \(s=1/2\).
The proton’s intrinsic magnetic moment points in the same direction as its intrinsic spin angular momentum because of the positive charge proton. This is contrasted with the negatively charged electron, where the spin and magnetic moment point in opposite directions.
Nuclear magnetic moments are measured in units of the nuclear magneton \(\mu_{\rm N}\), which is analogous to the Bohr magneton for electrons, by the relation
Note
The divisor in calculating \(\mu_{\rm N}\) is the proton mass \(m_p\) (rather than the electron mass), which makes the nuclear magneton \({\sim}1800\times\) smaller than the Bohr magneton.
The proton magnetic moment is measured as \(\mu_p = 2.79\mu_{\rm N}\). This contrasts strongly with the magnetic moment of the electron, \(\mu_e = -1.00116\mu_{\rm B}\). The neutron is electrically neutral, but is also has a magnetic moment, \(\mu_n = -1.91 \mu_{\rm N}\). The negative sign indicates that the magnetic moment points oppostie to the neutron spin.
Nucleons are more complicated structurally than electrons is shown by the large deviation from unity of the proton’s magnetic moment and the neutron having a magentic moment. The nonzero neutron magnetic moment implies that the neutron has negative and positive internal charge components at different radii, and hence a complex internal charge distribution.
11.2.2. Nuclear Magnetic Resonance#
Nuclear magnetic resonance (NMR) is an application that takes advantage of the nuclear magnetic moment’s response to large applied magentic fields. NMR can be applied to any nuclei that have instrinsic spin, proton (or hydrogen) NMR is used today more than any other kind. It is also the simplest to understand. Isidor Rabi, Edward Purcell, and Felix Bloch all played major roles in developing NMR, and received Noble Prizes in Physics for their efforts.
In proton NMR, a sample containing hydrogen atoms is placed in a strong magnetic field. With the magnetic field on, the sample is immersed in radio radiation with the frequency steadily varied.
When this applied radiation’s frequency \(f\) reaches the point at which the photon’s energy \(hf\) matches the energy difference between the split nuclear states,
the proton “flips” from the lower energy state to the higher one, and there is a sharp increase (resonance) in photon absorption.
The resonance frequency depends on the proton’s environment due to the shielding effect of surrounding electrons. As a result, a spectrum of photon absorption as a function of frequency provides a reliable signature of the sample’s content.
Physicists have developed techniques to utilize NMR in the studey of molecules and crystals through spectroscopy. All issues contain hydrogen, and the vastly different compositions of cells (e.g., bone, muscle, connective tissue, etc.) provide contrasting NMR responses that are turned into sharp images. This is done noninvasively with the application of low energy radiation \(({\sim}\rm \mu eV)\) that does little (or no) damage to human cells. Contrast this with x-ray imaging, with energies of \(1\ {\rm keV}\) or greater, which can seriously damage cells.
11.3. The Deuteron#
The next simplest nucleus (after the proton) is the deuteron \(\rm ^2H\). A deuteron consists of one proton and neutron, which allows us our first look at the nuclar force.
Let us determine how strongly the neutron and proton are bound together in a deuteron. The deuteron mass is \(2.013553\ {\rm u}\), and the mass of a deuterium atom (adding the electron) is \(2.014102\ {\rm u}\). The difference in masses is just the mass of an electron. The electron binding energy is so mall that it can be neglected.
The deuteron nucleus is bound by an energy \(B_d\), which represents mass-energy. The mass of a deuteron is then
The deuteron mass is less than the sum of the masses of a neutron and proton by just the nuclear binding energy \(B_d\). If we add an electron mass to each side of the equation, we have
The left hand side \((m_d + m_e)\) is the atomic deuterium mass \(M({\rm ^2H})\) and \(m_p + m_e\) is the atomic hydrogen mass (if we neglect the small amount of binding energy). Then we have
and we can use atomic masses.
Note
The electron masses cancel in almost all nuclear-mass difference calculations, where we routinely use atomic masses rather than nuclear masses. Also, we use uppercase \(M\) for atomic masses and lowercase \(m\) for nuclear and particle masses.
The binding energy \(B_d\) of the deuteron is determined using:
Using \({\rm u} = 931.5\ {\rm Mev/c^2}\), we convert the above mass-difference to energy by
Neglecting the atomic electron binding energy \((13.6\ {\rm eV})\) was justified, given that the nuclear binding energy is \(2.2\ {\rm MeV}\) (or \({\sim}10^6\) times greater). Even for heavier nuclei, we normally neglect the electron binding energies.
The binding energy of any nucleus \(\rm ^A_ZX\) is the energy required to separate the nucleus into free neutron and protons. It can be determined using the atomic masses by
We can check our result for the \(2.22-{\rm MeV}\) binding energy of the deuteron by using a nuclear reaction. We scatter gamma rays (i.e., photons) from deuterium gas and look for the breakup of a deuteron into a neutron and proton:
This type of reaction is called photodisintegration or a photonuclear reaction, because a photon causes the target nucleus to change form. The mass-energy relation is
where \(hf\) is the incident photon energy, \(K_n\) is the neutron kinetic energy, and \(K_p\) is the proton kinetic energy. If we want to find the minimum energy required for the photodisintegration, we let \(K_n = K_p = 0\). We then find
The above equation is not quite correct, because momentum must also be conserved in the reaction (\(K_n\) and \(K_p\) can’t both be zero). The precise relation is
This value of \(hf_{\rm min}\) is almost exactly \(B_d\), the deuteron binding energy, because the second term is so small. Experiment shows that a photon energy less than \(2.22\ {\rm MeV}\) cannot dissociate a deuteron.
Another striking property of a deuteron is its nuclear spin quantum number of \(1\). This indicates the neuteron and proton spins are aligned parallel to each other. The nuclear magnetic moment of a deuteron is \(0.86\mu_{\rm N}\), which is close to the sum of the free proton and neutron: \(2.79\mu_{\rm N} - 1.91\mu{\rm N} = 0.88\mu{\rm N}\). This supports our hypothesis of parallel spins.
11.4. Nuclear Forces and Stablity#
11.4.1. Nuclear Force#
The most straightforward technique to measure nuclear forces are based on scattering experiments. In scattering neutrons from protons, a deuteron is sometimes formed in the nuclear reaction:
The angular distribution of neutrons elastically scattered by protons (e.g., neutron + proton and proton + proton scattering) reveals that the nuclear potential is shaped with a deep well followed second potential. In the case of proton + proton scattering the second potential is the electrostatic interaction through the Coulomb potential.
The internucleon potential has a “hard core” that prevents the nucleon centers from approaching each other much closer than \({\sim}0.5\ {\rm fm}\). A proton has a charge radius up to \({\sim}1\ {\rm fm}\), where the neutron radius is about the same size.
Two nucleons within \({\sim}2\ {\rm fm}\) of each other feel an attractive nuclear force, whereas outside \(3\ {\rm fm}\) the nuclear force is essentially zero. The nuclear force is short range because it falls to zero so abruptly with interparticle separation. As a result, nucleons mostly interact with their nearest-neighbor nucleons.
The nuclear force is saturable because the interior nucleons are completely surrounded by other nucleons with which they interact. Nucleons on the nuclear surface are not completely bound, and their nuclear force is not saturated.
The only difference between the \(np\) and \(pp\) potentials is the Coulomb potential for \(r\geq 3\ {\rm fm}\) for the \(pp\) force. Inside \(3\ {\rm fm}\), the nuclear force clearly dominates, where outside \(3\ {\rm fm}\) only the Coulomb force is effective. The depth of the nucleon-nucleon potential is about \(40\ {\rm MeV}\); the \(np\) potential is slightly greater because of the absence of the Coulomb force.
The nuclear force is spin dependent because the bound state of the deuteron has the neutron and proton spins aligned, but there is no bound state with the spins anti-aligned.
The \(nn\) system is more difficult to study because free neutrons are not stable and decay. Indirect evidence along with analyses of experiments where moving neutrons scatter from each other indicates the \(nn\) potential is similar to the \(np\) potential. The nuclear potential between two nucleons seems independent of their charges, or the charge independence of nuclear forces.
For many purposes, the neutron and proton can be considered different charge states of the same particle. This is why we use the term nucleon to refer to either neutrons or protons.
11.4.2. Nuclear Stability#
If the binding energy of a nuclide \(B\) is positive, then the nuclide is stable against dissociating into free neutrons and protons. More generally, a nucleus containing \(A\) nucleons is stable if its mass is smaller than that of nay other possible combination of \(A\) nucleons. The binding energy of a nucleus \(^A_ZX\) against dissociation into any other possible combination of nucleons (e.g., \(R\) and \(S\)) is
The energy required to remove one proton (or neutron) from a nuclide is called the proton (or neutron) separation energy, where the above equation is useful for finding this energy. Even if \(B\) is negative, there may be other reasons why the nucleus is stable.
Exercise 11.4
Show that the nuclide \(\rm ^8Be\) has a positive binding energy but is unstable with respect to decay into two \(\alpha\) particles.
If one plots the known nuclides with neutron number \(N\) versus the proton number \(Z\), a trend of stable nuclides (i.e., line of stability) appears that is surrounded by a broader region of unstable nuclei.
It appears that for \(A\leq 40\), nature prefers the number of protons and neutrons in the nucleus to be about the same, \(Z=N\). For \(A > 40\), there is a preference for \(N>Z\).
We can understand this through the strength of the nuclear force that is independent of whether the particles are \(nn\), \(np\), or \(pp\). Equal numbers of neutrons and protons may give them most attractive internucleon nuclear force, but the Coulomb force must be considered as well. As the number of protons increases, the Coulomb force between all the protons becomes stronger until eventually affects the binding energy.
The electrostatic energy required to contain a charge \(Ze\) eveny spread throughout a sphere of radius \(R\) can be calculated by determining the work required to bring the charge inside the sphere from infinity (i.e., potential energy). This energy is
For a single proton, the self-energy is
This term represents the work done to assemble the proton itself, where we do not want to include it in the calculation of the electrostatic self-energy of a nucleus composed of \(Z\) protons. Therefore, we subract \(Z\) such terms from the total to get
Exercise 11.5
Show that Eq. (11.19) can be written as
and use this equation to calculate the total Coulomb energy of \(\rm ^{238}_{\ \ 92}U\).
For heavy nuclei, the nucleus will have a preference for fewer protons than neutrons because of the large Coulomb repulsion. There are no stable nuclei with \(Z>83\) because of the increasingly larger Coulomb force. The heaviest known stable nucleus is \(\rm ^{200}{\ \ 83}Bi\). All nuclei with \(Z>83\) and \(A>209\) will eventually decay spontaneously into some combination of smaller masses.
Adding one proton to a heavy nucleus adds a constant amount of nuclear binding energy, but the energy due to the repulsive Coulomb force increases twice as fast, \(\Delta E_c \sim (Z+1)^2 - Z^2 \approx 2Z\). Because the Coulomb force is long range, the proton interacts with all the protons already in the nucleus. As a result, nuclei with higher \(Z\) eventually become unstable. The neutrons dilute the Coulomb repulsion slightly because they intersperse among the protons, causing protons to be slightly farther apart.
The most stable nuclides have both even \(Z\) and even \(N\) (called “even-even” nuclides). Only four stable nuclides (all light nuclei) have odd \(Z\) and odd \(N\) (called odd-odd nuclides). These nuclides are \(\rm ^2H\), \(\rm ^6Li\), \(\rm ^{10}B\), and \(\rm ^{14}N\). All other nuclides are odd-even or even-odd.
Neutrons and protons are distinguishable fermions; hence they obey the Pauli exclusion principle. Only two neutrons (or protons) many coexist in each spatial orbital (i.e., quantum state), with spin up or down. Each nuclear energy level is able to hold two particles, the spins of which are paired to 0. Placing the same number of particles in any other arrangement will produce a less stable state of higher energy. Therein lies the preference for even \(N\) and \(Z\).
Niels Bohr, Carl F. von Weizsäcker and ohters were able (in the 1930s) explain many nuclear phenonmena using the liquid drop model, where they treated the nucleus as a collection of interacting particles in a liquid drop.
In 1935 von Weizsäcker proposed a semi-empirical mass formula based on the liquid drop model. Written in terms of the total binding energy, the semi-emipirical mass formula is
The volume term \((a_{\rm V})\) indicates that the binding energy is approximately the sum of all interactions between the nucleons. Because the nuclear force is short range and each nucleon interacts only with its nearest neighbors, this interaction is proportional to \(A\) (the total number of nucleons).
The second term (called the surface effect) is simply a correction to the first term because the nucleons on the surface are not completely surrounded by other nucleons. The surface nucleons do not have saturated interactions and a correction should be made proportional to the liquid drop surface area \((4\pi R^2)\). Because \(R\sim A^{1/3}\), the correction is proportional to \(A^{2/3}\).
The third term is the Coulomb energy.
The fourth term id due to the symmetry energy. In the absence of Coulomb forces, the nucleus prefers to have \(N\approx Z\). Notice that this term is independent of the sign of \(N-Z\).
The last term is due to the pairing energy and incorporates the fact that the nucleus is more stable for even-even nuclides. We can determine this empirically.
There have been many sets of parameters presented over time, where one set of parameters is:
where \(\Delta = 33\ {\rm MeV}\cdot A^{-3/4}\).
The entire table of stable isotopes can be understood by applying the ideas in the von Weizsäcker semi-empirical mass formula. Nuclides heavier than \(\rm ^{238}U\) must have decayed so quickly that quantities sufficient to measure no longer exist.
Many of the nuclides between \(\rm ^{209}Bi\) and \(\rm ^{238}U\) are still found in nature, either because
their decay rates are slow enough that they have not sufficiently decayed since their formation in the interior of stars, or
they are produced continuously by the radioactive decay of another nuclid.
To compare the relative staiblity of different nuclides, it’s important to know the binding energy per nucleon. The binding energy per nucleon can be determined by finding the binding energy of each known nucleus and dividing by its mass number.
Exercise 11.6
Calculate the binding energy per nucleon for \(\rm ^{20}_{10}Ne\), \(\rm ^{56}_{26}Fe\), and \(\rm ^{238}_{\ \ 92}U\).
11.5. Radioactive Decay#
Marie Curie and her husband Pierre discovered polonium and radium in 1898. Many nuclei are unstable and can decay spontaneously to some other combination of \(A\) nucleons that has a lower mass. These decays take different forms.
The simplest is that of a \(\gamma\) ray which represents the nucleus changing from an excited state to a lower energy state (no change in \(N\) or \(Z\)).
Other modes of decy include emission of \(\alpha\) particles, \(\beta\) particles, protons, neutrons, and fission.
The general form to law of radioactivity is the same for all decays because it is a statistical process. Given a sample of radioactive material we measure the disintegrations (or decays per unit time), which we define as activity. If we have \(N\) unstable atoms of a material, the activity \(R\) is given by
where we insert the minus sign to make \(R\) positive; \(dN/dt\) is negative because the total number \(N\) decreases with time. The SI unit of activity is the becquerel \((1\ {\rm Bq} = 1\ {\rm decays/s})\). In the past the unit was the curie \((\rm Ci)\) which is \(3.7\times 10^{10}\ {\rm decays/s}\).
Note
A typical radioactive source used in a student laboratory experiment (e.g., \({\rm ^{226}Ra}\) or \({\rm ^{210}Po}\) \(\alpha\) emitters), the \(\rm ^{241}Am\ \alpha\) emitter used in a smoke alarm, or the radium used in a luminous watch may have an activity of \({\sim}10^4\ {\rm Bq}\) (a few \(\rm \mu Ci\)).
The activity of a given sample falls of exponentially with time. If \(N(t)\) is the number of radioactive nuclei in a sample at time \(t\), and \(\lambda\) (decay constant) is the probability per unit time that any given nucleus will decay. Then the activity \(R\) is
The number \(dN\) of nuclei decaying during the time interval \(dt\) is
If we rearrange and integrate this equation, we have
If we let \(t=0\), then \(N(0) = C = N_o\) defines the initial number of radioactive nuclei in the sample. The equation becomes
This is the radioactive decay law, and it applies to all decays. The exponetial decay rate is consistent with experimental observation. The activity \(R\) is
where \(R_o\) is the initial activity at \(t=0\). The activity of a radioactive sample falls of exponentially.
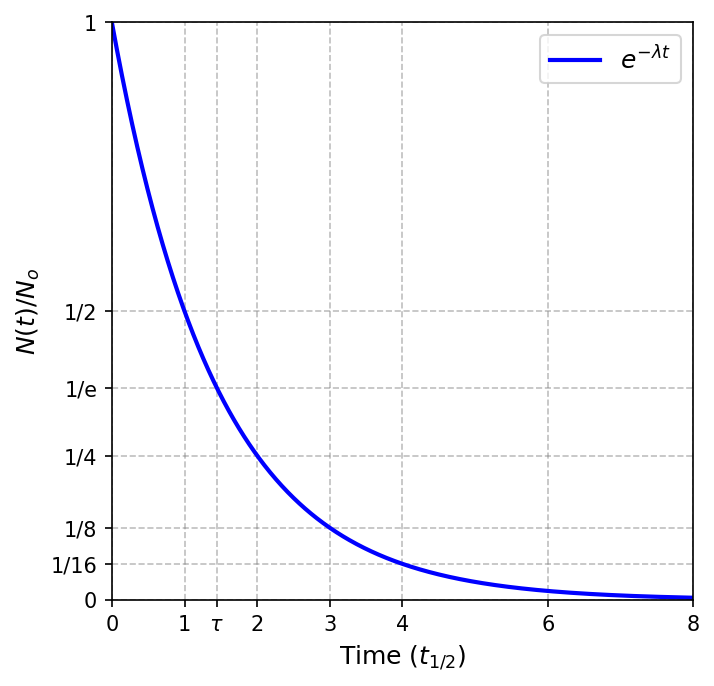
It is common to refer to the mean lifetime \(\tau\) (or half-life \(t_{1/2}\)) rather than its decay constant. The half-life is the time it takes one-half of the radioactive nuclei to decay. Mathematically, this is
The half-life is determined as
The mean (or average) lifetime \(\tau\) is calculated as
The python code below creates a plot showing the fraction of remaining nuclei \(N(t)/N_o\) as a function of the half-life \(t_{1/2}\) for a sample of radioactive nuclides. The mean lifetime \(\tau\) is indicated as well.
Note
Because radioactive decay is a statistical process, it will take a very large smaple to give a curve as smooth as the one shown here.
import numpy as np
import matplotlib.pyplot as plt
def decay_law(lam,t):
#normalized decay law e^(-lam*t)
return np.exp(-lam*t)
lam = 1#half-life; set to unity for this example
t_half = np.log(2)/lam
t = np.arange(0,8,0.01)*t_half #timescale in terms of the half-life
Norm_decay = decay_law(lam,t)
fs = 'large'
fig = plt.figure(figsize=(5,5),dpi=150)
ax = fig.add_subplot(111)
ax.plot(t/t_half, Norm_decay,'b-',lw=2,label = '$e^{-\lambda t}$' )
ax.set_yticks([0,0.0625,0.125,0.25,np.exp(-1),0.5,1])
ax.set_yticklabels(['0','1/16','1/8','1/4','1/e','1/2','1'])
ax.set_xticks([0,1,1/np.log(2),2,3,4,6,8]) #tau = 1/(ln 2)
ax.set_xticklabels(['0','1','$\\tau$','2','3','4','6','8'])
ax.set_ylim(0,1)
ax.set_xlim(0,8)
ax.grid(True, linestyle='--',color='gray',alpha=0.5)
ax.legend(loc='best',fontsize=fs)
ax.set_ylabel("$N(t)/N_o$",fontsize=fs)
ax.set_xlabel("Time ($t_{1/2}$)",fontsize=fs);
The three common decay modes of nuclei (\(\alpha,\ \beta,\ \gamma\)) were all observed by the early 20th century. When a nucleus decays, all the conservation laws must be observed: mass-energy, linear momentum, angular momentum, and electric charge. We add another conservation law for radioactive decay, called the conservation of nucleons.
The total number of nucleons (\(A\), the mass number) must be conserved in a low-energy nuclear reaction (e.g., less than \(938\ {\rm MeV}\)) or decay.
Neutrons can be converted into protons (and vice versa), but the total number of nucleons remains constant. At higher energies, an ample amount of rest energy is available to create nucleons, but other conservation laws still apply.
Radioactive decay can occur for a nucleus when some other combination of the \(A\) nucleons has a lower mass. Consider a parent radioactive nucleus \(^A_ZX\) with a mass \(M(^A_ZX)\). Two or more products can be produced in the decay. In the case of two products, let the mass of the lighter one by \(M_y\) and the heavier one (called the daughter) be \(M_D\). The conservation of energy is
where \(Q\) is the energy released (or disintegration energy) and is equal to the total kinetic energy of the reaction products.
Note
The disintegration energy \(Q\) is the negative of the binding energy \(B\). The binding energy normally refers to stable nuclei, whereas \(Q\) is normally used with unstable nuclei.
11.5.1. Alpha Decay#
The nucleus \(\rm ^4He\) is particularly stable, with a binding energy of \(28.3\ {\rm MeV}\). The combination of two neutrons and tow protons is strong because of the pairing effects. If the last two protons and neutrons in a nucleus are bound by less than \(28.3\ {\rm MeV}\), then the emission of an \(\alpha\) particle (alpha decay) is energetically possible. For alpha decay, we have
If \(Q>0\), then alpha decay is possible.
Consider the nucleus for \({\rm ^{230}_{\ \ 92}U}\). The alpha deacay reaction is given by
If we look up the appropriate masses (see isotopes of Uranium and isotopes of Thorium), we find
Alpha decay is allowed because \(Q>0\). The mass of the products is less than the mass of the decaying nuclide. Many nuclei (\(A>150\)) are susceptible to alpha decay.
You might why any nuclei exist with \(A>150\).
Neuclei are not necessarily made up of a collection of \(\alpha\) particles. Two neutrons and protons group together within the nucleus prior to the decay.
The alpha particle has great difficulty overcoming the nuclear attraction from the remaining nucleons to escape.
The barrier height \(V_B\) for alpha particles is normally \(>20\ {\rm MeV}\). The kinetic energies of alpha particles emitted from nuclei range from \(4-10\ {\rm MeV}\). It is classically impossible for the alpha particles to escape because the potential energy is greater than the kinetic energy.
The alpha particle is repelled by the Coulomb force if we project \(5-{\rm MeV}\) alpha particles onto a heavy nucleus, where it doesn’t get close enough to feel the attraction of the strong force. How can the alpha particle ever surmount the barrier if it is trapped inside the potential barrier?
The alpha particles are able to tunnel through the barrier. From quantum mechanics, there is a small (but finite) chance for the alpha particle to appear on the other side of the barrier. The probability depends on the barrier height and width. A more energetic alpha particle has a higher probability of tunneling, where this higher probability corresponds to a shorter lifetime for the nuclide.
Consider the \(\alpha\) decay of \(\rm ^{238} U\). The \(\alpha\) particle must make about \(10^{41}\) traverses (back and forth) across the nucleus before it can escape because of the low tunneling probability. We calculate the kinetic energy of the \(\alpha\) particle from the disintegration energy \(Q\).
Assume the parent nucleus is initially at rest so that the total moementum is zero.
The final momenta of the daughter \(\vec{p}_D\) and \(\alpha\) particle \(vec{p}_\alpha\) have the same magntidue and opposite directions.
Using the conservation of energy and linear moementum, we can determine the energy for the \(\alpha\) particle
Because the parent mass \(A\) is normally \(>150\), the \(\alpha\) takes most of the kinetic energy.
11.5.2. Beta Decay#
In alpha decay, the parent nucleus reverts to a daughter nucleus that is down 2 units in neutron number \(N\) and to the left \(2\) units in atomic number \(Z\). \(\alpha decay\) leaves the daugter nucleas farther from the line of stability than the parent.
Unstable nuclei can move closer to the line of stability by undergoing beta \((\beta)\) decay. The simplest example is the decay of a free neutron
Electrons cannot exist within the nucleus, when \(\beta\) decay occurs the \(\beta^-\) (electron) is created at the time of the decay. Note that \(\rm ^{14}C\) is unstable, where it has an excess of neutrons. We expect the beta decay of \(\rm ^{14}C\) to form \(\rm ^{14}N\) by
The emitted electron \((\beta^-)\) from the beta decay of \(\rm ^{14}C\) produces a continuous energy spectrum up to a maximum energy in contrast to the \(\alpha\) decay process that produces a monoenergetic spectrum. The measurement of a energy spectrum for beta decay was a problem for many years.
In addition to the energy sprectrum problem, there was a problem with spin conservations. In neutron decay, the neutron (spin \(1/2\)) cannot decay to two spin \(1/2\) particles (proton and electron). Note that \(\rm ^{14}C\) has spin \(0\), \(\rm ^{14}N\) has spin \(1\), and the electron has spin \(1/2\). We cannot combine spin \(1/2\) and \(1\) to make a spin of \(0\).
Both the electron energy spectrum and the spin angular momentum conservation posed major difficulties with our understanding of beta decay.
Wolfgang Pauli suggested (in 1930) that a third particle (called a neutrino) must also be produce in \(\beta\) decay. The neutrino (denoted by \(\nu\)) is a fermion (spin quantum number of \(1/2\)) with \(0\) charge$, and carries away the additional energy for energy conservation.
The neutrino has mass (although extremely small), where its energy is almost all kinetic. The photon cannot be the the missing particle because it has spin \(1\). Pauli’s suggestion seemed to explain the difficulties, and all circumstantial evidence available at the time supported the neutrino hypothesis. The detection of the neutrino was elusive until 1956 where Clyde Cowan and Frederick Reines made the discovery.
Neutrinos interact weakly with ordinary matter, and they pass right throught the Earth with little chance of being absorbed. They have no charge and do not interact electromagnetically. They are not affected by the strong force either. Beta decay is the product of the weak interaction, where neutrinos are created.
There are also antineutrinos (denoted by \(\bar{\nu}\)) as well as neutrinos. The beta decay of a free neutron and of \(\rm ^{14}C\) are correctly written as
where the antineutrino has \(-1/2\) spin.
The general forms of \(\beta^-\) decay and its disintegration energy are written as
The atomic mass of the parent and daughter nucleus are much larger than the \(\bar{\nu}\), so it can be neglected. When using atomic masses, the number of electron masses are already accounted. For \(\beta^-\) to occur, we must have \(Q>0\). In \(\beta^-\) decay, the \(Z\) changes to \(Z+1\) while the nucleus \(A\) stays constant. As a result, it is the unstable nuclei to the left of the line of stability that are moving closer to the line of stability.
For unstable nuclides with too many protons (i.e., to the right of the line of stability) another type of beta decay can occur with a positively charged electron (positron). In beta decay the electron and positron are denoted as \(\beta^-\) and \(\beta^+\), respectively.
Current experimental evidence suggests that a free proton does not decay, where the lower limit for the half life is much longer than the age of the universe \(t_{1/2}> 10^{27}\ {\rm yr}\). But a proton bound within the nucleus can transumtate if energy is taken from the nucleus and the result is a more stable nucleus. The isotope \(\rm ^{14}O\) is unstable and decays through \(\beta^+\) decay by:
The general forms of \(\beta^+\) decay and its disintegration energy are given as
In this case the electron masses do not cancel when atomic masses are used. The mass of the positron is equal to that of an electron.
There is another form of beta decay. Inner \(K\)- and \(L\)-shell electrons are tightly bound and their (classical) orbits are highly elliptical. As a result, these electrons spend a reasonable amount of time passing through the nucleus, which increases the possibility of atomic electron capture. A proton in the nucleus absorbs the electron, which produces a neutron and a neutrino in the process. The reaction for a proton is
The general forms of electron capture and its disintegration energy are given as
When one of the inner atomic electrons is captured, another electron will takes its place and produces a characteristic atomic x-ray. X-ray radiation in the absence of any other kind of radiation is a signature of electron capture. X-rays can also be produced in other kinds of nuclear decay where the decay products (i.e., \(\alpha\) particle) may knock out electrons during escape.
Electron capture has the same effect as \(\beta^+\) (or positron) decay, where a proton is converted into a neutron. Electron capture occurs more frequently for higher-\(Z\) nulclides because the inner atomic electron shells are more tightly bound.
11.5.3. Gamma Decay#
Uranium-230 can alpha decay to the ground state or any of the low-lying excited states of \(\rm ^{226}Th\). If the decay proceeds to an excited energy state of energy \(E_x\) rather than the ground state, then the disintegration energy \(Q\) (from the excited state to the ground state) can be determined. Let the disintegration energy to the ground state be \(Q_o\), such that the transition to the excited state \(E_x\) is related to the disintegration energy \(Q\) by
The distintegration value \(Q\) for the \(\alpha\) decay of \(\rm ^{230}U\) to \(\rm ^{226}Th\) can be determined using the energy of an excited state \(E_x = 0.072\ {\rm MeV}\) and \(Q_o = 5.992\ {\rm MeV}\). Therefore the disintegration energy \(Q\) is
A nucleus has excited states, but the exitation energies tend to be much larger (many \(\rm keV\) or even \(\rm MeV\)) due to the stronger nuclear interaction. One way for the nucleus to get rid of the extra energy is to emit a photon (i.e., \(\gamma\) ray) and undergo a transition to some lower energy state.
The gamma ray difference of the upper energy state \(E_u\) and the lower one \(E_l\) is
To conserve momentum, the nucleus must absorb some of this energy difference. However, a nuclues at rest is usually a very good approximation.
The decay of an excited state of \({^A}X^*\) (using \(*\) for the excited state) to the ground state is denoted by
where a transition between two excited states is denoted by
The excited energies (or levels) are characteristic of each nuclide. The gamma rays are normally emitted soon after the nucleus is created in an excited state.
We can contrast nuclear spectroscopy with that for the optical spectra of atoms. The solution of the Schrödinger equation for the Coulomb force of the atom is possible, but no such success has yet been obtained for the nuclear force. Therefore no encompassing theory exists that can predict certain characteristics of excited nuclear levels.
11.6. Radioactive Nuclides#
Our best cosmological evidence suggests that in the beginning (whatever time that is), there was a tremendous explosion (i.e., Big Bang) that released a huge amount of energy. Neutrons and protons condensed out of this energy cloud and after it was cool enough (after the first few minutes), they fused together to form deuterons and other light nuclei. The heavy elements would be formed by nuclear reactions within stars and by the death of stars through supernovae.
Unstable nuclei found in nature exhibit natural radioactivity, where those radioactive nuclides made in a lab exhibit artificial radioactivity (which includes all nuclides heavier than \(\rm ^{238}U\)). There are many natural radioactive nuclides left on Earth with lifetimes long enought to be observed.
Only those with half-lives longer than \({\sim}100\ {\rm Myr}\) have survived since primordial times. Table 11.1 shows some of the naturally occurring radioactive nuclides with their half-lives (in \(\rm Gyr\)) and natural abundance (in mole percentage).
Nuclide |
\(t_{1/2}\ ({\rm Gyr})\) |
Natural Abundance |
|---|---|---|
\(\rm ^{40}_{19}K\) |
\(1.28\) |
\(0.01\%\) |
\(\rm ^{87}_{37}Rb\) |
\(48\) |
\(27.8\%\) |
\(\rm ^{113}_{\ \ 48}Cd\) |
\(9 \times 10^6\) |
\(12.2\%\) |
\(\rm ^{115}_{\ \ 49}In\) |
\(4.4 \times 10^5\) |
\(95.7\%\) |
\(\rm ^{128}_{\ \ 52}Te\) |
\(7.7 \times 10^{15}\) |
\(31.7\%\) |
\(\rm ^{130}_{\ \ 52}Te\) |
\(2.7 \times 10^{12}\) |
\(33.8\%\) |
\(\rm ^{138}_{\ \ 60}La\) |
\(110\) |
\(0.09\%\) |
\(\rm ^{144}_{\ \ 60}Nd\) |
\(2.3 \times 10^{6}\) |
\(23.8\%\) |
\(\rm ^{147}_{\ \ 62}Sm\) |
\(110\) |
\(15.0\%\) |
\(\rm ^{148}_{\ \ 62}Sm\) |
\(7 \times 10^{6}\) |
\(11.3\%\) |
Heavy nuclides can change their mass number only by \(\alpha\) decay (\({^AX} \rightarrow {^{A-4}D}\)), but can change their charge number \(Z\) by either alpha or beta decay. There are only four paths that the heavy naturally occurring radioactive nuclides may take as they decy to stable end products.
The four paths have mass number expressed by \(4n\) up to \(4n + 3\) (\(n= \text{integer}\)) because only alpha decay can change the mass number. The four radioactive series are listed in Table 11.2, where neptunium is the only unnatural radioactive series.
Mass Numbers |
Series Name |
Parent |
\(t_{1/2}\ ({\rm Gyr})\) |
End Product |
|---|---|---|---|---|
\(4n\) |
Thorium |
\(\rm ^{232}_{\ \ 90}Th\) |
\(14\) |
\(\rm ^{208}_{\ \ 82}Pb\) |
\(4n+1\) |
Neptunium |
\(\rm ^{237}_{\ \ 93}Np\) |
\(0.00214\) |
\(\rm ^{209}_{\ \ 83}Bi\) |
\(4n+2\) |
Uranium |
\(\rm ^{238}_{\ \ 92}U\) |
\(4.47\) |
\(\rm ^{206}_{\ \ 82}Pb\) |
\(4n+3\) |
Actinium |
\(\rm ^{235}_{\ \ 92}U\) |
\(0.704\) |
\(\rm ^{207}_{\ \ 82}Pb\) |
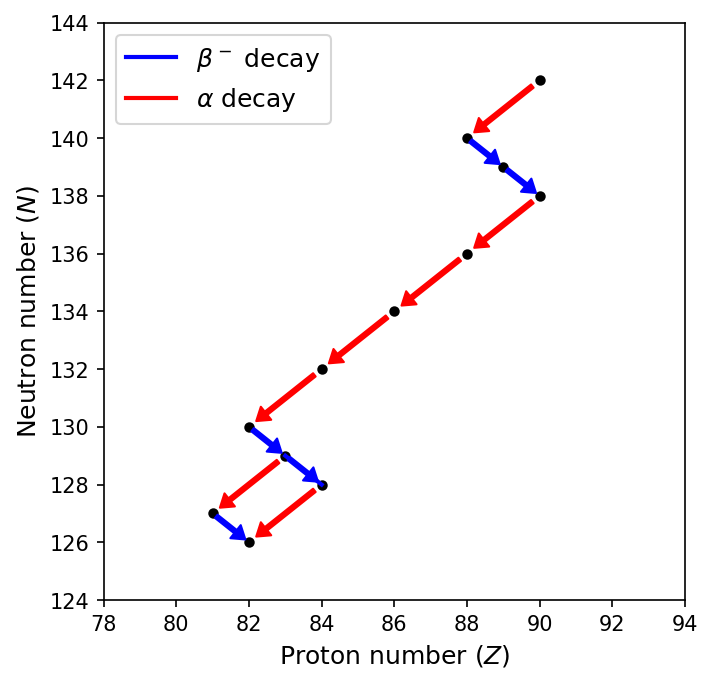
The sequence of \(\rm ^{232}Th\) is shown in the figure below. Note that \(\rm ^{212}_{129}Bi\) can decay either \(\alpha\) or \(\beta^-\) decay, which is called branching. Normally one path of the branch is highly favored, but both paths are shown because it has a \(36\%\) probability of \(\alpha\) decay and a \(64\%\) probability for \(\beta^-\) decay. The overall effect of the successive decays is to bring the nuclide closer to the line of stability until a stable nuclide is finally reached.
import numpy as np
import matplotlib.pyplot as plt
charge_number = np.array([90,88,89,90,88,86,84,82,83,81,82,84])
Atomic_number = np.array([232,228,228,228,224,220,216,212,212,208,208,212])
neutron_number = Atomic_number - charge_number
npts = len(neutron_number)
fs = 'large'
fig = plt.figure(figsize=(5,5),dpi=150)
ax = fig.add_subplot(111)
ax.plot(charge_number,neutron_number,'k.',ms=8)
dx,dy,col = -2,-2, 'g'
for i in range(0,npts-2):
end = i+2
if end > npts:
end = npts
if (charge_number[i]-charge_number[i+1])>0:
col = 'r'
else:
col = 'b'
dx = np.diff(charge_number[i:end])
dy = np.diff(neutron_number[i:end])
ax.annotate('',xy=(charge_number[i+1], neutron_number[i+1]), xytext=(charge_number[i], neutron_number[i]),arrowprops=dict(color=col, shrink=0.1,width=2,headwidth=8,headlength=6))
ax.plot([83,84],[129,128],'b-',lw=2,label='$\\beta^-$ decay')
ax.annotate('',xy=(84, 128), xytext=(83, 129),arrowprops=dict(color='b', shrink=0.1,width=2,headwidth=8,headlength=6))
ax.plot([84-0.5,82+0.5],[128-0.5,126+0.5],'r-',lw=2,label='$\\alpha$ decay')
ax.annotate('',xy=(82, 126), xytext=(84, 128),arrowprops=dict(color='r', shrink=0.1,width=2,headwidth=8,headlength=6))
ax.legend(loc='best',fontsize=fs)
ax.set_xlim(78,94)
ax.set_ylim(124,144)
ax.set_yticks(np.arange(124,146,2))
ax.set_xlabel("Proton number ($Z$)",fontsize=fs)
ax.set_ylabel("Neutron number ($N$)",fontsize=fs);
11.6.1. Time Dating using Lead Isotopes#
The isotope \(\rm ^{204}Pb\) is not radioactive and no other nuclide decays to it, which makes its abundance presumably constant. Two other stable isotopes (\(\rm ^{206}Pb\) and \(\rm ^{207}Pb\)) are at the end of the radioactive chains of \(\rm ^{238}U\) and \(\rm ^{235}Pb\), respectively.
The ratio of \({\rm ^{207}Pb}/{\rm ^{204}Pb}\) has been relatively constant over the past \(2\ {\rm Gyr}\). Most of the \(\rm ^{235}U\) has already decayed to \(\rm ^{207}Pb\) because Uranium-235 has a relatively short half-life (\(0.7\ {\rm Gyr}\)) compared to the age of the Earth. The half-life of \(\rm ^{238}U\) is so long, where the ratio of \({\rm ^{206}Pb}/ {\rm ^{204}Pb}\) is still increasing.
A plot of the abundance ratio of \({\rm ^{206}Pb}/ {\rm ^{204}Pb}\) vs. \({\rm ^{207}Pb}/{\rm ^{204}Pb}\) can be a sensative indcator of the age of lead ores (see the Holmes-Houtermans System for Lead Isochrons). Such techniques have shown that some meteorites are \({\sim}4.5\) billion years old (or \({\sim}4500\ {\rm Ma}\)). This is in agreement with dating measurements on Moon rocks returnd to Earth. No \(4.6\ {\rm Gyr}\) old rocks have yet been found on Earth, but indirect evidence (through embedded zircons) strongly suggest that the Earth formed \({\sim}4.5\ {\rm Gyr}\) ago.
11.6.2. Radioactive Carbon Dating#
Radioactive \(\rm ^{14}C\) is produced in out atmosphere by the bombardment of \(\rm ^{14}N\) by neutrons by cosmic rays through
A natural equilibrium of \(\rm ^{14}C\) to \(\rm ^{12}C\) exists for molecules of \(\rm CO_2\) from the atmosphere, where all living organisms use or breathe that \(\rm CO_2\). When living organisms die, their intake of \(\rm ^{14}C\) ceases and the ratio \({\rm ^{14}C}/{\rm ^{12}C}\ (=R)\) decreases as \(\rm ^{14}C\) decays.
To use \(\rm ^{14}C\) for dating, corrections must be made for the changes in Earth’s atmospheric composition and for variations in the cosmic ray flux due to changes in Earth’s magnetic field.
At the time of death, the initial decay rate is \(14\ {\rm decays/min/g}\) of carbon, or \(R=1.2\times 10^{-12}\). This method has been calibrated using tree-ring counting for samples up to about 10,000 years old. It is convenient to use carbon dating to determine the ages of objects over a wide range up to \({\sim}60,000\) years ago because the half-life of \(\rm ^{14}C\) is \(5730\) years. The uncertainty increases dramatically for times greater than 10,000 years ago.
11.7. Nuclear Reactions#
Rutherford used \(7.7\)-\({\rm MeV}\) alpha particles from the decay of \({\rm ^{214}_{\ \ 84}Po}\) to bombard a nitrogen target, where he observed the protons being emitted. He was not certain of the exact nuclear reaction taking place, but he convinced himself that a nuclear transformation took place. The reaction was
The first nucleus written is the projectile, where the second is the target and is normally at rest. These two nuclei interact and undergo a transmutation to one or more final particles. The detected particle is normally listed first after the arrow, and the residual nucleus listed last.
A short hand way of writing the above reaction is
The gneraly reaction \(x + X \rightarrow y + Y\) is written in shorthand as
Isotopes of hydrogen are written using \(p,\ d,\ t\) in place of the more cumbersome \(\rm ^1H\), \(\rm ^2H\), and \(\rm ^3H\). The stable helium-4 nucleus is denoted by \(\alpha\). These shorthand symbols are used when they are the projectile or detected particle.
The study of nuclear reactions was helpd by three important technological advances in accelerator development:
These three accelerators (and the ones that followed) allowed nuclear reactions to be studied in the lab using accelerated particles of controlled energy and intensity. This allowed detailed study of specific characterstics of the nucleus.
Nuclear photodisintegration is the initiation of a nuclear reaction by a photon.
Neutron or proton radiative capture occurs when the nucleon is absorbed by the target nucleus, with energy and momentum conserved by \(\gamma\)-ray emission.
An asterisk \(*\) denotes when a particle’s nucleus is in an excited state.
The projectile and target are in the entrance channel of a nuclear reaction.
The reaction products are in the exit channel.
In elastic scattering the entrance and exit channels are identical and the particles in the exit channels are not in excited states. In inelastic scattering, the entrance and exit channels are also identical, but one (or more) of the reaction products in the exit channel are left in an excited state. The products and also not be in an excited state as well. Examples of this are
11.7.1. Cross Sections#
The properties of the nucleus have mostly been determined by detecting the particle(s) in the exit channel. The probability of a particular nuclear reaction occurring is determined by measuring the cross section \(\sigma\) (see Rutherford Scattering).
The cross section is calculated by measuring the number particles produced in a given nuclear reaction. For the cross section, we let
Then the number of target nuclei \(N_s\) is
The probability of the particle begin scattered is proportional to the cross section times the total number of target nuclei \(N_s\). We compute a normalized product as
The product \(nt\) is the number of target nuclei exposed per unit area.
We measure the cross section by counting the number of detected particles as a function of the number of incoming particles. If the cross sections are measured as a function the scattering angle \(\theta\), then we call them differential cross sections \(\sigma(\theta)\).
Differential cross sections are determined by the number of particles scattered into a small solid angle \(d\Omega\) (measured in units of steradian \(\rm sr\)) surrounding the scattering angle \(\theta\). In spherical coordinates, the solid angle is \(d\Omega = \sin{\theta}\ d\theta d\phi\).
The differential cross section can also be written as \(d\sigma/d\Omega\), which measures the number of particles per differential solid angle. Integrating the differential cross section over the entire range of scattering angles yields the total cross section \(\sigma_T\),
The cross sections depend on the incident kinetic energy, as well as other properties (e.g., spins). They are traditionally measured in units of barns (\(\rm b\)) with \(1\ {\rm barn} \equiv 10^{-28}\ {\rm m^{2}} = 100\ {\rm fm^2}\).
11.8. Reaction Kinematics#
For low-energy nuclear reactions, the kinetic energies are typically much lower than the rest energies. Therefore, we can use the non-relativistic kinematics in most cases.
Consider the reaction \(x + X \rightarrow y + Y\), where the momentum and kinetic energy of the projectile \(x\) are \(\vec{p}_x\) and \(K_x\), respectively. The target is assumed to be at rest, so \(\vec{p}_X = K_X = 0\).
The conservation of energy for the reaction is
If we rearrange the above equation to separate the masses and kinetic energies, we find an expression similar to the disintegration energy:
The difference between the final and initial kinetic energies is precisely the difference between the initial and final mass energies, which we call the Q value (or energy release).
Nuclear masses are required, but we may use atomic masses.
The electron masses cancel.
The electron binding energies are small, so we neglect their differences.
Energy is released in a nuclear reaction when \(Q>0\) (exoergic, or exothermic). When \(Q<0\), the kinetic energy is converted to mass-energy (endoergic, or endothermic).
In an elastic collision: \(x+X \rightarrow x+ X\), we must have \(Q=0\).
In an inelastic collision: \(x+X \rightarrow x + X^*\), we must have \(Q<0\).
An endoergic reaction will not occur unless there is enough kinetic energy \(K_x\) to supply the required nuclear rearrangement energy. The energy must be available in the center-of-mass (\(cm\)) system where \(v_{cm} = 0\); the total momentum in the \(cm\) is zero.
The minimum kinetic energy needed to initiate a nuclear reaction is the threshold energy \(K_{th}\), where the particles \(y\) and \(Y\) will be at rest in the \(cm\) system . Particle \(y\) will be moving in the lab system.
The speed of the center of mass is given by
The speeds of \(x\) and \(X\) in the center-of-mass system (denoted by prime \(^\prime\)) are
At threshold, we must have \(v_y^\prime = v_Y^\prime = 0\) in the center-of-mass system. The conservation of energy in the center-of-mass system is
Since \(v_y^\prime = v_Y^\prime = 0\) at threshold, we have (using Eq. (11.53))
which reduces to
Substituting for the threshold energy \(K_{th} = \frac{1}{2}M_xv_x^2\), we have
11.9. Reaction Mechanisms#
The primary technique for studying nuclei and nuclear forces was through scattering reactions. Physicists measure cross sections that are proportional to the reaction probabilities, which depend on nuclear structure.
There are different types of reactions that occur over different bombarding energies. Reactions initiated by electrons differ from those initiated by \(\alpha\) particles.
The scattering for heavy charged particles (protons and \(\alpha\) particles) at low energies (\(E<10\ {\rm MeV}\)) is dominated by the Coulomb force and the compound nucleus reaction mechanism is appropriate.
For bombarding energies between \(10-100\ {\rm MeV}\), direct reactions are more appropriate.
For \(E>140\ {\rm MeV}\), a new particle (a pion) emerges, which interacts strongly with the nuclear force.
Energies from \({\sim}200-1000\ {\rm MeV}\) is the realm of medium-energy physics that has experiments dominatied with protons, pions, and electrons.
Above \({\sim}1\ {\rm GeV}\) is the domain of high-energy physics.
11.9.1. The Compound Nucleus#
Niels Bohr proposed that nuclear reactions take place through formation and decay of a compound nucleus. This compound nucleus is a composite of the projectile and target nuclei, usually in a high state of excitation.
A compound nucleus \(CN\) is formed by \(x\) and \(X\) in the entrance channel with an excitation energy
In the \({\rm ^{12}C}(\alpha,\ n){\rm ^{15}O}\) reaction, enough energy is available from just the masses to leave \(\rm ^{16}O^*\) in an excited state with \(7.2\ {\rm MeV}\) when an \(\alpha\) particle and carbon-12 join together. The kinetic energy available in the center-of-mass \(K_{cm}^\prime\) is
which can excite the compound nucleus to even higher excitation energies than that from just the masses.
The compound nucleus can exist for a relatively long time compared with the time taken by the bombarding particle to cross the nucleus. This latter time is referred to as the nuclear timescale \(t_N\).
For a \(5\ {\rm MeV}\) proton (\(v\approx 0.1c\)) crossing a typical nuclear diamter of about \(9\ {\rm fm}\), the nuclear timescale is \({\sim}3\times 10^{-22}\ {\rm s}\). Compound nuclei can live for \({\sim}10^{-15}\ {\rm s}\) or \(10^6 t_N\).
Bohr’s hypothesis suggested that the nucleus “forgets” how it was forme, and the excitation energy is shared by all the nucleons in the nucleus. When the compound nucleus finally decays from its highly excited state, it decays into all possible exit channels according to statistical rules consistent with conservation laws.
Nuclei have discrete energy levels (similar to atoms), where the lowest state is called the ground state with \(0.0\ {\rm MeV}\). Considering the low-lying states of \(\rm ^{16}O\), first excited state is \(6.05\ {\rm MeV}\) and the next (closeby) state is \(6.13\ {\rm MeV}\).
Nuclear physicists vary the projectile bombarding energy \(K_x\) and measure the cross section \(\sigma_T\) at each energy (generally at fixed angles for the outgoing particles). This called an excitation function. Sharp peaks in the excitation function of the reacting particles are called resonances, and they represent a quantum state of the compound nucleus being formed (e.g., interaction of \(\alpha + {\rm ^{12}C} \rightarrow n + {\rm ^{16}O^*}\)).
This explains why \({\rm ^{12}C}(\alpha,\ n){\rm ^{15}O}\) has such a large cross section. The reaction populated a resonance near \(E({\rm ^{16}O^*}) = 18.2\ {\rm MeV}\). The quantum numbers of \({\rm ^{12}C}(\alpha,\ n){\rm ^{15}O}\) exit channel select this energy level in \(\rm ^{16}O^*\) to be populated, where as the quantum numbers for the \({\rm ^{12}C}(\alpha,\ p){\rm ^{15}N}\) exit channel do not.
The uncertainty principal can be used to relate the energy width of a particular nuclear state \(\Gamma\) to its lifetime \(\tau\), or
If the width of a measured nuclear state is \(\Gamma\) (using an excitation function), then the above equation can be used to determine its lifetime. Ground states for stable nuclei have zero energy width, and hence an infinite lifetime.
Neutrons have zero net charge, where they interact more easily with nuclei at low energies than do charged particles. If the nuclide \(\rm ^{113}_{\ \ 48}Cd\) interacts with a neutron, the compound nucleus \(\rm ^{113}_{\ \ 48}Cd^*\) may be formed. We call this process neutron activation.
One mode for decay of this compound nucleus is the emission of a \(\gamma\) ray. The reaction \({\rm ^{113}_{\ \ 48}Cd}(n,\ \gamma){\rm ^{114}Cd}\) is an example of neutron radioactive capture, which produces \(\gamma\) ray energies that are characteristic of the energy-level structure of the \({\rm ^{114}Cd}\) nucleus. They are like a unique fingerprint that indicates the original presence of \({\rm ^{113}_{\ \ 48}Cd}\). The general technique is called neutron activation analysis, which can be used to identify elements without damaging the samle.
The neutron capture reaction \((n,\ \gamma)\) often has a large cross section, which can be 1000s of \({\rm barns}\) at a resonance. As neutrons pass through matter, they lose energy by having many collisions. They eventually reach a (thermal) kinetic energy \(3kT/2\) when they attain thermal equilibrium with their surroundings.
The average neutron capture cross section varies empircally with the neutron’s velocity as \(v^{-1}\). The inverse-velocity dependence is explained in terms of the time the neutron spends near the nucleus (i.e., \(t = 2r/v\), where \(2r\) is the nuclear diameter). The longer the neutron is within the range of the nuclear force, the more likely it will be captured.
11.9.2. Direct Reactions#
As the energy of the bombarding particle rises, the excitation energy of the compound nucleus is higher. The compound nuclear excited states become broad (large \(\Gamma\)), and the number of nuclear statees becomes very large. As the state lifetimes decrease, they approach that of the nuclear timescale.
The compound nucleus states overlap, where the idea of a compound nucleus loses its utility to analyze reactions. If a compound nucleus state is formed, it is very likely to emit one (or more) nucleons (i.e., neutrons) to get rid of the extra excitation energy. Nucleon decay will almost always occur before \(\gamma\) decay when the conservation laws allow it.
For higher bombarding energies, the bombarding particle spends much less time within the range of the nuclear force. It becomes more probable to:
(a) strip one or more nucleons off the projectile, or
(b) pick up one or more nucleons from the target.
It is also possible to knock out energetic nucleons from the target nucleus, which are called direct reactions.
The advantage of direct reactions is that the final residual nucleus can be in any one low-lying excited states. By using different direct reactions, the nuclear excited states can be studied in many ways to learn about nuclear structure.
11.10. Fission#
Nuclei with \(A=56\) have the highest average binding eneriby, where some nuclei with \(A>100\) can alpha decay and many nuclei with \(A>220\) can readily fission into two separate fragments. One fragment is typically somewhat larger than the other.
Fission occurs foor heavy nuclei beacuse of the increased Coulomb forces between protons. We can understand fission through the semi-empirical mass formula based on the liquid drop model (see Eq. (11.21)).
For a spherical nucleus (with mass number \(A{\sim}240\)), the attractive short-range nuclear forces (volume term) more than offset the Coulomb repulsive term.
As a nucleus becomes nonspherical (deformed), the surface energy is increased and the short-range nuclear interactions are reduced.
Nucleons on the surface are not surround by other nucleons, and the unsaturated nuclear force reduces the overall nuclear attraction. For a particular level of deformation, the fission barrier is overcome, which corresponds to a critical energy. In the liquid drop model, this corresponds to the when the Coulomb force pushes a deformed drop apart.
A careful examination of Eq. (11.21) reveals that spontaneous fission occurs for nuclei with \(Z^2/A\geq 49\ (Z\approx115,\ A\approx 270)\). The ratio \(Z^2/A\) comes from the surface energy and Coulomb energy terms. Spontaneous fission can also occur for \(Z^2/A < 49\) through tunneling, but the half-lives are much longer.
The naturally occuring nuclide with the highest spontaneous fission rates is \(\rm ^{238}U\), which has a half-life for fission of \(8.2 \times 10^6\ {\rm Gyr}\). The alpha decay half-life is only \(4.5\ {\rm Gyr}\), which means that \(\rm ^{238}U\) is a million times more likely to alpha decay than to fission.
11.10.1. Induced Fission#
Fission may also be induced by a nuclear reaction. A neutron abosrbed by a heavy nucleus forms a highly excited compound nucleus that may quickly fission. An example of induced fission is
The fission producs have a ratio of \(N/Z\) that is too high to be stable for their \(A\) value. Normally \(2-3\) neutrons are emitted during fission. There are many possibilities fo the \(Z\) and \(A\) of the fission products.
Symmteric fission (products with equal \(Z\)) is possible.
The most probable fission is asymmetric (one mass larger than the other).
11.10.2. Thermal Neutron Fission#
The binding energy per nucleon of \(\rm ^{236}U\) is about \(7.6\ {\rm MeV}\), where the binding energy per nucleon of the fission fragments is about \(8.4\ {\rm MeV}\). Due to the difference in binding energies, the energy released per nucleon is \(0.8\ {\rm MeV}\). The total energy released is \(236\ \text{nucleons} \times 0.8\ {\rm Mev/nucleon} \approx 190\ {\rm MeV}\).
We can use the liquid drop model to understand how fission can be induced so easily in havey nuclei. When \(\rm ^{235}U\) absorbs a thermal (low-energy) neutron to form \(\rm ^{236}U^*\), the excitation energy is \(6.5\ {\rm MeV}\). This nucleus is in a highly-excited and unstable state, which makes is susceptible to deformation. It becomes so deformed that the Coulomb force overcomes the nuclear force, and the nucleus separates (much like a liquid drop).
Experiments show that \(\rm ^{235}U\) and \(\rm ^{239}Pu\) fission easily after absorbing thermal neutrons. The nuclide \(\rm ^{238}U\) needs a neutron with a kinetic energy \(K\geq 1\ {\rm MeV}\) to easily fission. If lower energy neutrons are absorbed, the resulting exicted \(\rm ^{239}U^*\) is more likely to decay by emitting a \(\gamma\) ray. The cross section is larger for low energy neutrons because the cross section \(\sigma_T \propto v^{-1}\).
Fission fragments are highly unstable because they are so neutron rich. This occurs because heavy nuclei deviate more significantly from the \(N=Z\) line. After the fission, the resulting fission fragments are relatively futher away from the line of stability. Prompt neutrons are emitted simultaneously with the fissioning process.
Even after the prompt neutrons are released, the fission fragments undergo \(\beta\) decay and release more energy. Most the energy \({\sim}200\ {\rm MeV}\) released in fission goes into the kinetic energy of the heavier products, but the lighter particles (e.g., neutrons, \(\beta\) particles, neutrinos, and \(\gamma\) rays) typically carry away \(30-40\ {\rm MeV}\) of the kinetic energy.
11.10.3. Chain Reactions#
Neutrons produced via fission can produce fissions with other nuclei. This is the basis of the self-sustaining chain reaction.
A critical mass of fissionable material must be present to increase the chances of a neutron being absorbed.
If at least one neutron (on average) results in another fission, the chain reaction becomes critical.
If less than one neutron (on average) produces another fission, the reaction is subcritical.
If more than one neutron (on average) produces another fission, the reaction is supercritical.
An atomic bomb is an extreme example of a supercritical fusion reaction.
A critical-mass fission reaction can be controlled by absorbing neutrons. A self-sustaining controlled fission process dpeends on the fact that not all neutrons are prompt. Some of the neutrons are delayed by several seconds adn are emitted by daughter nuclides resulting from the (slow) \(\beta\) decay of the fission fragments. These delayed neutrons allow the control of a nuclear reactor with control rods that absorb neutrons to sustain a controlled reaction.
11.10.4. Fission Reactors#
Nuclear fission is a useful energy source for commerical power production (see Table 11.3).
Material |
Amount |
Energy \((\rm MJ)\) |
|---|---|---|
Coal |
\(1\ {\rm kg}\) |
\(30\) |
Oil |
\(1\ {\rm barrel}\ (160\ {\rm l})\) |
\(6000\) |
Natural gas |
\(1\ {\rm ft^3}\ (28\ {\rm l})\) |
\(1\) |
Wood |
\(1\ {\rm kg}\) |
\(10\) |
Gasoline |
\(1\ {\rm gal}\ (3.8\ {\rm l})\) |
\(100\) |
Uranium (fission) |
\(1\ {\rm kg}\) |
\(10^7\) |
The fuel requirements for a \(1000\ {\rm MW}\) power plant is \({\sim}8\times 10^6\ {\rm kg}\) of coal (1 trainload/day), where the requirement for uranium-fission is only \(3\ {\rm kg}\).
Several components are important for a controlled nuclear reaction:
Fissionable fuel
Moderator to slow down neutrons
Control rods for safety and to control the criticality of the reactor
Reflector to surround the moderator and fuel to contain neutrons (and improve efficiency)
Reactor vessel and radiation shield
Energy transfer systems to deliver the power commercially
Uranium-235 fissions with thermal neutrons, where only \({\sim}2.5\) neutrons (on average) result from each fission; It is important not to lose neutrons. Two main effects can “poison” reactors: (1) neutrons can be absorbed without producing fission and (2) neutrons may escape from the fuel zone.
To produce a critical mass of \(\rm ^{235}U\), we must process natural uranium ore to enrich the uranium-235 content \((0.7\%)\) from the more abundant \(\rm ^{238}U\) \((99\%)\). Current power reactors require uranium-235 enrichment of \(4-5%\).
Fission neutrons typically have \(1-2\ {\rm MeV}\) of kinetic energy, where slowing down these nuetrons helps increaes the chance of producing another fission by increasing the cross section. A moderator is used to elastically scatter the high-energy neutrons and reduce their energies. Hydrogen (in water), carbon (graphite), and beryllium have been used as moderators.
If commercial power is desired, reactor designers must add a method to transfer energy. The most common method is to pass hot water heated by the reactor through some form of heat exchanger.
In boiling water reactors (BWRs) the moderating water turns into steam, which drives a turbine producing electricity.
In pressurized water reactors (PWRs) the moderating water is under high pressure and circulates from the reactor to an external heat exchangeiner where it produces steam, which drives a turbine.
BWRs are inherently simpler than PWRs, but the possibility that the steam driving the turbine may become radioactive is greater with the BWR. The two-step process of the PWR helps to isolate the power generation from possible radioactive contamination.
Research reactors are operated to produce high neutron fluxes for neutron scattering experiments. Smaller reactors (\(100\ {\rm MW}\)) operate in Russia for heat production to warm both homes and businesses. Other reactors are designed to produce radioisotopes for industrial and medical purposes.
A promising choice for an advanced kind of reactor is the breeder reactor, which provides more fissionable fuel than it consumes. When \(\rm ^{238}U\) undergoes the \((n,\ \gamma)\) reaction, the resulting \(\rm ^{239}U\) beta decays into \(\rm ^{239}Np\) which itself beta decays into \(\rm ^{239}Pu\) via the reaction chain
Ther resulting plutonium-239 has a half-life of \(24,100\ {\rm yr}\) and is an \(\alpha\) emitter. THe intermediate beta decays take place in a matter of days. The plutonium is easily separated from the uranium by chemical means, where the plutonioum fissions easily with both thermal and fast neutrons.
Thermal neutrons are those in equilbrium with their environment and have \(\lesssim 1\ {\rm keV}\) of energy. Fast neutrons have energies up to a few \(\rm MeV\).
11.11. Fusion#
The only primary souce in widespread use that is not derived from the Sun is nuclear power. Energy emitted by stars arises from nuclear fusion reations in which light nuclei fuse together. This process contrasts with nuclear fission, in which large nuclei divide.
When \(\rm ^{236}U^*\) fissions, it divides into nuclei with a larger binding energy per nucleon, thereby releasing energy. If two light nuclei fuse together, they alos form a nucleus with a larger binding energy per nucleon and energy is released.
The most energy is released if two isotopes of hydrogen (deuteron and triton) fuse toghether in the reaction
About \(3.5\ {\rm MeV}\) per nucleon is released because of the stron binding of \(\rm ^4He\). Less than \(1\ {\rm MeV}\) per nucleon is released in fission.
11.11.1. Formation of Elements#
In the first few minutes of the universe, the light elements of hydrogen and helium were formed. Millions of years later, the heavier elements were formed in stars through nuclear fusion. Thre are two main cycles for producing energy in stars.
The first is the proton-proton chain, which converts 4 protons into an \(\alpha\) particle. As stars form due to gravitational attraction, the heat (average speed of the protons) increases substantially so they can overcome their Coulomb repulsion (with the help of quantum tunneling) and fuse by the following reactions:
This reaction produces a deuteron \((\rm ^2H)\) and is a special kind of weak-interaction beta decay process. It is extremely slow, because only 1 collision in about \(10^{26}\) produces a reaction. This is good, otherwise the Sun would explode!
The deuterons that accumulate can combine with a proton \(\rm ^1H\) to produce \(\rm ^{3}He\):
The \({\rm ^3He}\) can then combine to produce \({\rm ^4He}\) through:
Note
The first two reactions which create the deuteron and helium-3 must occur more than once to produce the enough matter for the final reaction that produces helium-4.
A total of six \({\rm ^1H}\) are requred to produce \({\rm ^4He}\) and two \({\rm ^1H}\). This process consumes four protons. The total \(Q\) for 6 \({\rm ^1H}\) produce \({\rm ^4H}\) is \(24.7\ {\rm MeV}\), where an additional \(2\ {\rm MeV}\) come from the annihilation of two electron-positiron pairs for a total of \(26.7\ {\rm MeV}\).
The proton-proton chain is slow because Eq. (11.64) limits the entire process. As the reaction proceeds, the star’s temperature increases and eventually carbon-12 nuclei are formed through by the triple-alpha process (i.e., converting 3 \({\rm ^4He}\) into a \({\rm ^{12}C}\)).
Another cycle can produce the \({\rm ^4He}\), if enough carbon is produced (or already present) near the stellar core. The series of reactions responsible are called the CNO cycle:
Note
Four \({\rm ^1H}\) and one \({\rm ^{12}C}\) are required to produce \({\rm ^4He}\) and \({\rm ^{12}C}\). The {\rm ^{12}C} nucleus serves as a catlyst.
The proton-proton chain is probably responsible for most of our Sun’s energy production, but the CNO cycle is a much more rapid fusion reaction. It requires higher temperatures (\({\sim}2\times 10^7\ {\rm K}\)) than are present in the Sun, because of the higher Coulomb barrier of \({\rm ^{12}C}\) compared to the \({\rm ^1H}\) for the protons.
A hydrostatic equilibrium exists in the Sun between the gravitational attraction that contracts a star and a gas presssure that pushes out due to the fusion process. As the lighter nuclides are consumed to produce heavier nuclides, the gravitatioanl attraction succeeds in contracting the star’s mass into a smaller volume and the temperature increaes.
A higher temperature allows the nulcides with higher \(Z\) to fuse. This process continues until a large part of the Sun’s mass is converted to iron. Then the Sun collapses under its own graviational attraction to become a white dwarf. For more massive stars, they can contract more which allows them to become a neutron or black hole, but this is sensitive to the star’s initial mass.
11.11.2. Nuclear Fusion on Earth#
Some scientists beleive that controlled nuclear fusion is ultimatlely our best source of terrestrial energy. Among the several possible fusion reactions, three of the simplest involve the three isotopes of hydrogen:
Deuterium \(({\rm ^2H})\) exists in vast quantities in seawater. Assuming that there are \(10^{21}\ {L}\) of water on Earth, the natural abundance of deuterium \((0.015\%)\) gives \(10^{43}\) deuterons. These deuterons (when fused together to make \(\rm ^{3}He\)) would produce over \(10^{30}\ {\rm J}\) of energy. This is enough to support present world energy consumption for a few billion years.
Three main conditions are necessary for controlled nuclear fusion:
The temperature must be hot enough to allow the ions (e.g., \(d\) and \(t\)) to overcome the Coulomb barrier and fuse thier nuclei together. This requires a temperature of \(100-200\) million \(\rm K\).
The ions must be confined to a small volume to allow the ions to fuse. A suitable ion density is \(2-3 \times 10^{20}\ {\rm ions/m^3}\).
The ions must be held together in close proximity at high temperature long enough to avoid plasma cooling, where a suitable time is \(1-2\ {\rm s}\).
The suitable values given above assume magnitic confinement. The product of the plasma density \(n\) and the containment time \(\tau\) must have a minimum value at a sufficiently hgih temperature to initiate fusion and produce as much energy as it consumes. The minimum value is
The above relation is calle dthe Lawson criterion. A triple product of \(n\tau T\) called the fusion product is also sometimes use:
The factor \(Q\) is used to represent the ratio fo the power produced in the fusion reation to the power required to produce the fusion (heat). This \(Q\) factor is not to be confused with the \(Q\) value for the release of binding energy.
The breakeven point is \(Q=1\), and ignition occurs for \(Q\gg 1\). For controlled fusion produced in the laboratory, temperatures equivalent to \(kT = 20\ {\rm keV}\) are satisfactory. For uncontrolled fusion (i.e., a H-bomb), high temperatures and densities are acheived over a very brief time by using a fission bomb. Fusion bombs do not produce radiation effects nearly as severe as those of fission bombs, because the primary products are not dangerously radioactive.
11.11.3. Controlled Thermonuclear Reactions#
A controlled thermonuclear reaction of nuclear fusion in the laboratory is one of the primary goals of science and engineering. Scientists do not expect to reach this goal for several more decades. The first fusion reaction will likely be the \(D + T\) reaction. The tritium will be derived from two possible reactions:
The lithium is required to generate the tritium. It is also used as the heat transfer medium and a neutron radiation shield.
For \(Q=1\), a product of a few times \(10^{21}\ {\rm s\cdot keV/m^3}\) will be required for a commercial reactor using \(D+T\). There are two major schemes to control thermonuclear reactions:
Magnetic confinement fusion (MCF), and
Inertial confinement fusion (ICF).
The primary effort of research laboratories around the world for several years has been a device called the tokamak. As many as six separate magnetic fields can be used to contain and heat the plasma.
In a schematic cross section of a typical magnetic containment vessel,
The center is the location of the hot plasma where the \(D+T\) reaction takes place.
The plasma is surrounded by vaccum to keep out impurities that would poison the reaction.
A wall surrounds the plasma and vacuum region, which would be subjected to intense radiation. The plasma must be kept from touching the enclosure.
A lithium blanket is the next layer, which absorbs neutrons to breed more tritium.
Next is a radiation shield to prevent radiation from reaching the magnets, which may be superconducting in a commerical reactor.
The heating of the plasma to sufficiently high temperatures begins with the resistive heating from the electric current flowing in the plasma. This is insufficient to attain the high ignition temperature. As a result, there are two other schemes to add additional heat: (1) injection of high-energy \((40-120\ {\rm keV})\) neutral fuel atoms that interact with the plasma, and (2) radio-frequency (RF) induction heating of the plasma (similar to a microwave oven).
The most significant fusion project in the near future is a large tokamak fusion reactor called the ITER (International Thermonuclear Experimental Reactor). It is currently under construction in France and is expected to generate self-sustained fusion power of \(500\ {\rm MW}\) for \(1000\ {\rm s}\).
The concept of intertial confinement fusion is to use an intense high-powered beam of heavy ions or a laser called a driver to implode a pea-sized target composed of \(D+T\) to a density and temperature high enough to cause fusion ignition.
Several US-based institutions are doing research and development in laser fusion.
The National Ignition Facility (NIF) at Lawrence Livermore National Lab fires 192 lasers in to a high-Z cylinder, which produces x-rays. These x-rays heat the small fuel pellet containing the \(D+T\). It produced \(1.3\ \rm MJ\) of UV laser energy in 2010, just short of the \(1.5\ {\rm MJ}\) needed for ignition.
Sandia National Lab used a device called a Z-pinch that uses a huge jolt of current to produe a powerful magnetic field that squeezes ions inot implosion and heats the plasma. Fracne is building a device called Laser Megajoule with similar objectives as the NIF.
11.12. Special Applications#
Particle beams, radioactive nuclides, and nuclear effects have many applications, where most depend on a specific isotope of radioactive element called a radioisotope. The usefulness of a given radioisotope may depend on the specific decay particle it produces, fission fragment, or even on the half-life. Radioisotopes are produced by different methods.
Particle accelerators as reaction products:
An important accelerator-produced radioisotope is \(\rm ^{68}Ga\), which is used in diagnostic medicine.
Nuclear reactors as fission fragments or decay products,
One important fission fragment is \(\rm ^{99}Mo\) that beta decays to \(\rm \mathbf{^{99m}Tc}\), where the \(\rm m\) indicates that it is a metastable nuclear isomer.
Nuclear reactors using neutron activation.
Neutron activation is used in many ways, from crime detection to the production of nuclides heavier than uranium-238.
Another important application is the the search for a very small concentration of a particular element called a trace element. Irradiating an object suspected of containing a trace element may produce a radioactive nucleus that has a particular decay.
11.12.1. Medicine#
Radioisotopes are useful in medical research, diagnostics, and treatment. Some \(\beta^-\) emitters (\(\rm ^3H\), \(\rm ^{14}C\), and \(\rm ^{32}P\)) are widely used in medical research. The most widely used is \(\rm ^{99m}Tc\), where it is used in about \(80\%\) of all nuclear medicine procedures.
Technetium-99m has a half-life of \(6\ \rm h\), where it produces a \(140\)-\(\rm keV\) gamma ray when it decays to the ground state of \(\rm ^{99}Tc\). A patient is given an intravenous injection of \(\rm ^{99m}Tc\), where it can be trapped in certain areas of the body. A few minutes after the injection, the patient is scanned for gamma rays to pinpoint the \(\rm ^{99m}Tc\) activity.
The nuclide \(\rm ^{99}Mo\) is produces as a fission product or as a by-product material in a nuclear reator. It is mostly produced by neturon bombardment of highly enriched uranium-235, which subsequently fissions. The \(\rm ^{99}Mo\) beta decays to form the useful \(\rm ^{99m}Tc\):
The radionuclide \(\rm ^{123}I\ (t_{1/2}= 13\ {\rm h})\) is useful for a thyroid function test, where it is produced by an accelerator in a reaction such as,
The iodine-123 decays via electron capture to excited states of \(\rm ^{123}_{\ \ 52}Te\) by
About \(98\%\) of the time a \(159\)-\(\rm keV\) gamma ray is produced, which is detected by an array of \(\rm NaI\) dectectors.
Radioisotopes are also used in tomography, which is a technique for displaying images of parts of the body to look for abnormal physiology or testing functional characteristics of organs. Tomography now includes varius techniques:
single-photon emission computed tomography (SPECT),
posititron emission tomography (PET),
magentic resonance imaging (MRI), and others.
In the first two techniques, the radiation (normally \(\gamma\) rays) is detected externally to determine the location of the radionuclide inside the body. The use of very short-lived radiopharmaceuticals has resulted in numerous accelerators placed in medical centers to produce the necessary radioisotopes.
11.12.2. Archaeology#
Apart from the use of \(\rm ^{14}C\), investigators can now measure a large number of trace elements in many ancient speciments. They compare the results looking a the concentrations to determine whether the specimens have the same origin. This technique has been used to examine pottery fragments excavated from the ancient Agora (in Athens) and from pyramids in Egypt.
To understand the people inhabiting the “New World”, scientist use carbon-dating on spear points and other tools to build a timeline of human migration. From these measurements, many experts believe that the first settlers crossed a land bridge over the Bering Strait from present-day Siberia to Alaska. Carbon-dating measurments indicate that humans had settlements near Clovis, NM about \(12,000\) years ago.
The Chauvet Cave (discovered in France in 1995) has more than 300 paintings, engravings, and other traces of human activity (e.g., hearths, flintstones, and footprints). From carbon-14 dating, these works are believed to be from the Paleolithic era (\({\sim}32,000\) years ago).
11.12.3. Crime Detection#
Neutron activation analysis helps investigators search for particular elements indicative of crime. The examination of gunshots by measuring trace amounts of barium and antimony from the gun powder is \(100-1000\times\) more sensitive than looking for residue itself. Using \((n,\ \gamma)\) techniques, as little as \(0.005\ {\rm \mu g}\) of barium and \(0.001\ {\rm \mu g}\) of antimony can be detected.
Scientists can detect toxic elements in hair by neutron activation analysis, where small amounts of arsenic and mercury can be detected. A famous study by several Scottish scientists examined samples of Napoleon’s hair taken during the last five years of his life and just after death.
The beta emitter \(\rm ^{76}As\ (t_{1/2} = 26.4\ h)\) was studied after being activated in a nuclear reactor. Analysis of the strands revealed that Napoleon had arsenic concentrations of \({\sim}40\times\) larger than normal. Some speculate that Napoleon was poised, but it was common for his physicisian to use arsenic in treating many illnesses.
11.12.4. Materials#
Historically, there has been a problem of radiation damage of an electronic device on a large single chip of silicon.
Alpha particle decay from a contaminant uranium or thorium nucleus could cause “soft” computer errors as it ionizes the silicon.
Cosmic ray particles can create similar problems, especially in satellites and space probes.
Fast-nueutron irradiation of bulk computer memory components can decrease the soft-error rate by a factor of \(10\). The neutrons reduce the intrinsic resisitivity in the silicon substrate so that the extraneous ionization caused later is much less likely to reset a bit.
Phosphorous-doped silicon can be produced with fast-neutron irradiation. Natural silicon consists of \(3.1\%\) of \(\rm ^{30}Si\), which undergoes the reaction
Because the \({\rm ^{31}Si}\) will be evenly distributed throughout the silicon, the phosphorous doping will also be much more uniformly distributed than could have been achieved by diffusive doping techniques. Silicon treated this way is called neutron-transmutation-doped silicon and is better able to handle high power levels in rectifiers.
Neutrons are used to study material properties due to the neutron’s small wavelength and zero charge, which allows it to easily probe atomic dimensions. Examples include:
crystal structures,
magnetic properties,
interatomic and lattice forces,
alloys,
structures and dynamics of liquids,
superconductors,
phase transitions, and
voids in materials (e.g., oil shale).
Neutrons are particularly useful because they do not ionize the material as do charged particles and photons. They penetrate matter easily and introduce unifor lattice distortions or impurities. Thermal neutrons have just the right momenta and energies to probe vibrational states, their acoustic moeds, and the underlying interatomic forces in solid lattices.
11.12.5. Small Power Systems#
Alpha emitting radioactive sources (e.g. \(\rm ^{241}Am\) or \(\rm ^{238}Pu\)) have been used as power sources in heart pacemakers. Smoke detectors use \(\rm ^{241}Am\) sources of alpha particles as current generators. The scattering of alpha particles by the smoke particles reduces the current flowing to a sensistive solid-state device which results in an alarm.
Spacecraft have been powered using radioisotope generators (RTGs) since the early 1960s. The devices use the heat produced by the \(\alpha\) decay of \(\rm ^{38}Pu\) to produce electricity in a thermocouple circuit. About 24 spacecraft have used RTGs (including Apollo, Pioneer 10/11, Viking 1/2, Voyager 1/2, Galileo, Ulysses, Cassini, Perserverance). Current RTGs supply almost \(300\ {\rm W}\) and usually more than one unit is placed on a spacecraft.
All past and present operational RTGs exceeded their original design requirements both in power output and longevity. Voyagers 1 and 2 were both launched in 1977, and their RTGs are both still operational in 2024 (40+ years later).


