1. Birth of Modern Physics#
1.1. Classical Physics of the 1890s#
The Renaissance brought the discoveries of Greek scholars (e.g., Aristotle, Eratosthenes, Pythagoras, etc.) back to the forefront of knowledge. Scientific progress during the Age of the Enlightenment developed the ideas from antiquity further as a result of the development of print and competition.
Investigating the natural world within a mathematical framework is a fundamental characteristic that we would call physics today. The knowledge and practice of physics was developing from using Euclidean geometry (e.g., Eratosthenes) to the development of Calculus (e.g., Newton and Leibniz). For the physicists of the 1890s, classical physics was a refined subject that appeared reliable despite the considerable changes occurring in the social, political, and intellectual realms of Western Europe.
“There is nothing new to be discovered in physics now. All that remains is more and more precise measurement.”
—William Thomson (Lord Kelvin) in 1900
Scientists and engineers of the late 19th century believed they had everything under control, where the best scientists of the day were highly recognized and rewarded. Basic research was recognized as important because of the commercial and military applications of those discoveries. The developments of visionaries (e.g., Nikola Tesla) caused many to take note of the business opportunities of scientific research. People and ideas began to travel quickly from one country to another as scientific journals were becoming more accessible. Classical physics developed some of the most important (and useful) principles that we still use today in the form of conservation laws.
The conservation laws describe fundamental properties of nature, where the initial and final quantities must be equal. The total volume of water in a gallon is independent of how many containers it fills. Mathematically, a conservation law of a quantity \(x\) held in \(j\) containers is:
where the superscripts \(i\) and \(f\) represent the initial and final states of the quantity, respectively.
The four main conservation laws are:
Conservation of energy: The total sum of energy (in all its forms) is conserved in all interactions.
Conservation of linear momentum: In the absence of external forces, linear momentum is conserved in all interactions.
Conservation of angular momentum: In the absence of external torques, angular momentum is conserved in all interactions.
Conservation of charge: Electric charge is conserved in all interactions.
A 19th century scientist might have added the conservation of mass to the list, but Einstein’s theory of special relativity shows that conservation of mass is intimately connected to conservation of energy (i.e., one of a few dualities in modern physics).
1.1.1. Mechanics#
The laws of mechanics were codified most famously by Isaac Newton, but many of the postulates and principles that we associate with mechanics were derived by others over centuries. Galileo was a great experimenter and engineer, where he
developed the concept for Inertia (i.e., Galilean relativity), and
built one of the first telescopes based on only seeing a design of a spyglass by Hans Lipperhey.
Galileo also discovered properties of a pendulum (at least for small amplitudes) and a relationship for falling objects (e.g., hammer and feather though experiment).
Isaac Newton expanded our present understanding of mathematics, astronomy, and physics. Within physics, he developed the fields that describe motion, forces, gravitation, optics, and thermodynamics. He understood the relationship between position (and displacement) with velocity as a rate of change (i.e., time derivative), which could be further applied to determine a body’s acceleration. A force applied is simply a mass that is accelerated and being at rest is the special case of no external forces or moving at constant velocity. The universality of the gravitational force was a huge development during his time, which showed that the heavens obeyed the same rules as the mortals (and apples) on Earth.
Newton described the relationship between net force and acceleration in three laws that bear his name today:
Newton’s first law: An object in motion with a constant velocity will continue in motion unless acted upon by some net external force. This is a restatement of Galileo’s inertia experiments with inclined planes. Newton’s first law is also called the law of inertia and is used to describe inertial reference frames.
Newtons second law: The acceleration \(\vec{a}\) of a body is proportional to the net external force \(\vec{F}\) and inversely proportional to the mass \(m\) of the body. Mathematically, it is stated as
Newton’s third law: The force exerted by body 1 on body 2 is equal in its magnitude and opposite in direction to the force that body 2 exerts on body 1. Let’s define the force on body 2 by body 1 as \(\vec{F}_{21}\), then Newton’s third law is written as
In this form, it is often called the law of action and reaction.
Newton’s law of motion develop the concept of force because a force is required to alter a body’s motion. The concepts of: velocity \(\vec{v}\), acceleration \(\vec{a}\), and linear momentum \(\vec{p}\) that are associated with force can be applied to rotation to get: angular velocity \(\vec{\omega}\), angular acceleration \(\vec{\alpha}\), and angular momentum \(\vec{L}\).
1.1.2. Electromagnetism#
Electricity and magnetism were developed over a long period of time with important contributions by
James Clerk Maxwell, and
Each of these contributions were held separately until Maxwell showed that electricity and magnetism were intimately connected. He also showed that electricity and magnetism were related through a change in the inertial frame of reference. Maxwell’s work led to the understanding of electromagnetic radiation, which describes the behavior of light. Maxwell combined the ideas of the time into four equations that form electromagnetism as
in 1865, Maxwell derived a force law for electromagnetism from Faraday’s law ((Huray (2010);Yaghjian (2019)) in A Treatise on Electricity and Magnetism. Hendrik Lorentz arrived at a complete derivation in 1895, which is
Maxwell’s equations show
a symmetry between electric and magnetic fields,
and
charges and currents create fields, which can in turn create other fields.
1.1.3. Thermodynamics#
Thermodynamics deals with the flow of energy through a temperature \(T\), heat \(Q\), work \(W\), and the internal energy of a system \(U\). These basic quantities come together to describe a pressure \(P\), volume \(V\), and entropy \(S\). Important contributions to thermodynamics were made by
Benjamin Thompson (Count Rumford),
Rudolf Clausius, and
William Thomson (Lord Kelvin).
The primary results of thermodynamics can be describe by two laws:
First law of thermodynamics: The change in the internal energy \(\Delta U\) of a system is equal to the heat \(Q\) added to the system plus the work \(W\) done on the system. The first law of thermodynamics generalized the conservation of energy by including heat. Mathematically it is written as
Second law of thermodynamics: It is not possible to convert heat completely into work without some other change taking place. In other words, “there’s no such thing as a free lunch”. Heat does not spontaneously flow from a colder body to a hotter body without some change taking place.
Two additional laws are sometimes expressed, which are
Zeroth law of thermodynamics: If two thermal systems are in thermodynamic equilibrium with a third system, they are in equilibrium with each other.
Third law of thermodynamics: It is not possible to achieve an absolute zero temperature.
1.2. Kinetic Theory of Gases#
Gases are composed of atoms and molecules in rapid motion that bounce off each other and the walls, but this had just gained acceptance in the 1890s. Coming to this realization came from many people, where Robert Boyle showed (~1862) that the product of the pressure and volume of a gas was constant, as long as the temperature was constant (i.e. \(PV = \text{constant}\), or Boyle’s law). Later, Jacques Charles found the ratio of the volume and temperature was constant, as long as the pressure was constant (i.e., \(V/T = \text{constant}\), or Charles’ law). Joseph Louis Gay-Lussac produced the same result as Charles around the same time.
1.2.1. Ideal gas law#
If we combine Boyle’s law with Charles’ law, we obtain the equation for an ideal gas, which is
which depends on the number of moles \(n\) of the gas and the ideal gas constant \(R = 8.31\ {\rm J/(mol \cdot K)}\).
Amedeo Avogadro proposed that equal volumes of gases at the same temperature and pressure contained an equal number of molecules. Daniel Bernoulli originated the kinetic theory of gases in 1738, but was generally ignored. However, by 1895 the kinetic theory of gases was widely accepted.
1.2.2. Statistical Thermodynamics#
The statistical interpretation of thermodynamics was made by Maxell, Ludwig Boltzmann, and Josiah Willard Gibbs.
In the simple theory of an ideal gas, an average over the collisions of many molecules reveals that the average kinetic energy \(\langle K \rangle\) of the molecules is linearly proportional to the temperature \(T\) and the internal energy \(U\). Mathematically, this is represented as
which depends on Avagadro’s number \(N_A = 6.02214076 \times 10^{23}\). This relation ignores the rotational or vibrational contributions to the molecular energy.
Energy is not represented only by translational motion, were it became clear that all degrees of freedom were capable of carrying energy. The equipartition theorem states that each degree of freedom for a molecule has an average energy \(kT/2\), where \(k\) is the Boltzmann constant \((k = R/N_A)\). Translating through 3D space introduces three degrees of freedom, where rotational and vibrational modes can also contribute to a higher temperature. Therefore, if there are \(f\) degrees of freedom, then Eqn. (1.7) becomes
The molar \((n=1)\) heat capacity \(C_V\) at constant volume for an ideal gas is the rate of change in internal energy with respect to the change in temperature, or
The experimental quantity of specific heat as a function of temperature for molecular hydrogen \({\rm H_2}\) is shown below, where the lowest level \(C_V = \frac{3}{2}R\) corresponds to only translational motion. At \(200\ {\rm K},\), the rotational degrees of freedom become important, \(C_V\) rises to \(\frac{5}{2}R\). Near \(3200\ {\rm K}\), the vibrational degrees of freedom bring \(C_V\) to \(\frac{7}{2}R\) before the molecule dissociates.
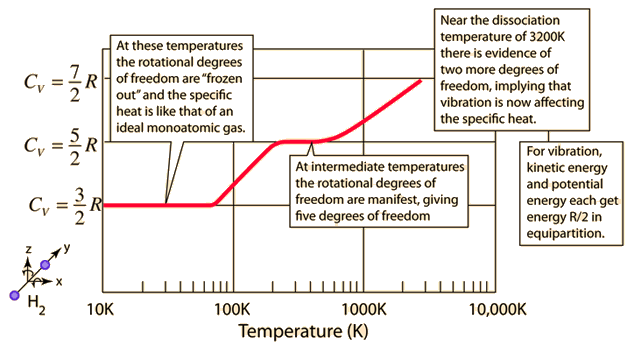
Fig. 1.1 Image Credit: Hyperphysics section for specific heat.#
1.2.3. Maxwell-Boltzmann Distribution#
In the 1850s, Maxwell derived a relation for the distribution of speeds of molecules in gases. The distribution of speeds \(f(v)\) depends on the mass of the molecule \(m\) and the temperature of the gas \(T\), which is given as
The python code below computes the Maxwell speed distribution for an \({\rm N_2}\) gas at temperatures of \(300,\ 1000,\ \text{and}\ 4000\ {\rm K}\). The peak of each distribution is the most probable speed of a gas molecule for a given temperature. This was not confirmed experimentally until 1921.
# Maxwell speed distribution for Nitrogen
import numpy as np # https://numpy.org/doc/stable/user/whatisnumpy.html
# https://docs.scipy.org/doc/scipy/reference/constants.html
from scipy.constants import k, physical_constants
import matplotlib.pyplot as plt # https://matplotlib.org/
def f_v(m, T, v):
# Maxwell speed distribution
# m = mass of a molecule in kg
# T = temperature of a gas in K
# v = velocity of molecules in m/s
return 4*np.pi*(m/(2*np.pi*k*T))**1.5*v**2*np.exp(-m*v**2/(2*k*T))
amu = physical_constants['atomic mass constant'][0]
m_N2 = 28*amu
T_low = 300 # Temperature of N_2 in K
T_mid = 1000 # Temperature of N_2 in K
T_hi = 4000 # Temperature of N_2 in K
v_N2 = np.arange(0, 4000, 10) # velocity range in m/s
fs = 'large'
fig = plt.figure(figsize=(4, 4), dpi=150)
ax = fig.add_subplot(111)
ax.plot(v_N2, f_v(m_N2, T_low, v_N2)*1000, '-', lw=2, label='300 K')
ax.plot(v_N2, f_v(m_N2, T_mid, v_N2)*1000, '--', lw=2, label='1000 K')
ax.plot(v_N2, f_v(m_N2, T_hi, v_N2)*1000, ':', lw=2, label='4000 K')
ax.legend(loc='best', fontsize=fs)
ax.set_xlabel("$v$ (m/s)", fontsize=fs)
ax.set_ylabel("$f(v)$ ($\\times 10^{-3}$)", fontsize=fs)
ax.set_ylim(0, 2)
ax.set_xlim(0, 4000);
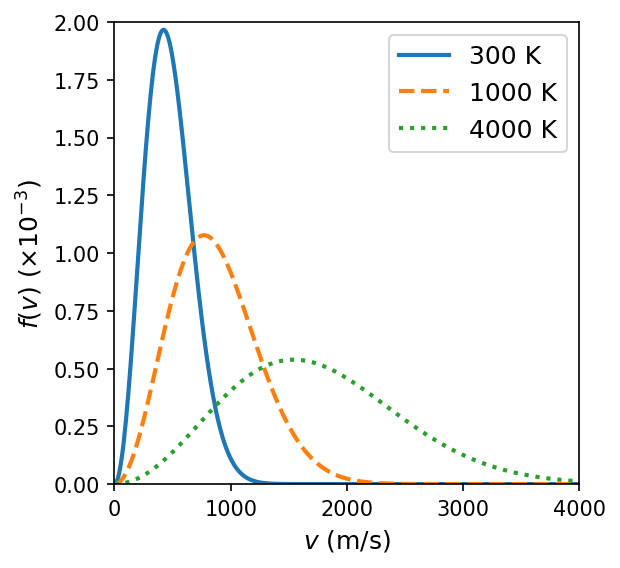
By 1895, Boltzmann had made Maxwell’s calculation more rigorous, where the relation became known as the Maxwell-Boltzmann distribution. The most probable speed can be used to find the root-mean-square speed \(v_{\rm rms}\),
1.3. Waves and Particles#
Point particles are a good model when we are first learning physics, however nature isn’t always that simple. Two- or three-dimensional models can become necessary when more precision is required to describe the interaction. Many natural phenomena can be explained as waves that are energy-carrying disturbances or standing waves that are superpositions of traveling waves. Most waves (e.g., water and sound) need an elastic medium in which to travel.
1.3.1. Energy Transport#
Matter is not transported in waves, but energy is. Mass doesn’t actually propagate along with the wave, where the mass moves in response to changes in energy as the wave passes. Consider the following examples,
A buoy on water As a water wave passes, the buoy gains gravitational potential energy as it moves up and releases it as gravity pulls it back down. The buoy helps the wave move by displacing the nearby water and the cycle continues.
Fans at a baseball game A wave can propagate through a stadium of baseball fans, as long as each column of fans stands up and sits down at the right time. A single fan doesn’t have to run around the whole stadium.
1.3.2. Waves or Particles?#
As early as the 17th century, waves and particles were a subject of disagreement (especially when talking about light). Newton supported the idea that light was composed of corpuscles (or particles), where geometrical optics uses straight-line, particle-like trajectories (i.e., rays) to explain observations of reflection and refraction. It could also explain the observation of sharp shadows.
Christiaan Huygens considered light as a wave phenomenon. the wave theory could explain reflection and refraction, but not the sharp shadows. Huygens poor health prevented him from continuing his work on the wave theory and Newton’s reputation carried the particle-like nature of light forward. Thomas Young performed his double-slit interference experiment, which indicated that light behaved as a wave. Figure 1.2 illustrates a plane wave encountering a double-slit to produce a diffraction pattern on the other side.

Fig. 1.2 Two-slit diffraction pattern by a plane wave. Image credit: wikipedia#
In the 1860s, Maxwell showed that electromagnetic (EM) waves consist of oscillating electric and magnetic fields. Visible light covers just a narrow range of the total EM spectrum, and all EM radiation travels at the speed of light \(c\) in free space, given by
The product of the wavelength \(\lambda\) and the wave frequency \(f\) defines the wave speed for any wave, including light. The fundamental constants for the permeability \(\mu_o\) and permittivity \(\epsilon_o\) of free space reveal the connection of the speed of light to the rest of nature. In 1887, Heinrich Hertz succeeded in generating and detecting EM waves having wavelengths far outside the visible range (\(\lambda \approx 5\ {\rm m}\)).
1.4. Conservation Laws and Fundamental Forces#
Conservation laws guide our deduction of the principle of physics, where the application of a few laws explains a huge swathe of the universe. Modern physics describes what we have learned within the last ~100 years. Prior to modern physics, mass and energy were distinctly different, but now we seem them connected through the conservation of mass-energy. The study of subatomic (or even elementary) particles, forces us to consider the conservation of baryons and leptons. Closely related to conservation laws are invariance principles, where describes that some observables can remain unchanged under some transformation (e.g., a measured distance is the same even if you translate the coordinate system).
1.4.1. Fundamental Forces#
Through the discoveries of modern physics, scientists developed a description of four fundamental forces (gravitational, electromagnetic, weak, and strong). All other forces that are described in your introductory physics course can be described as a derivative of these forces. Under very high energy, the electromagnetic and weak forces can unify into a single force called the electroweak force. Figure 1.3 shows the strength of each force scaled to the strong force that holds the atomic nucleus together.
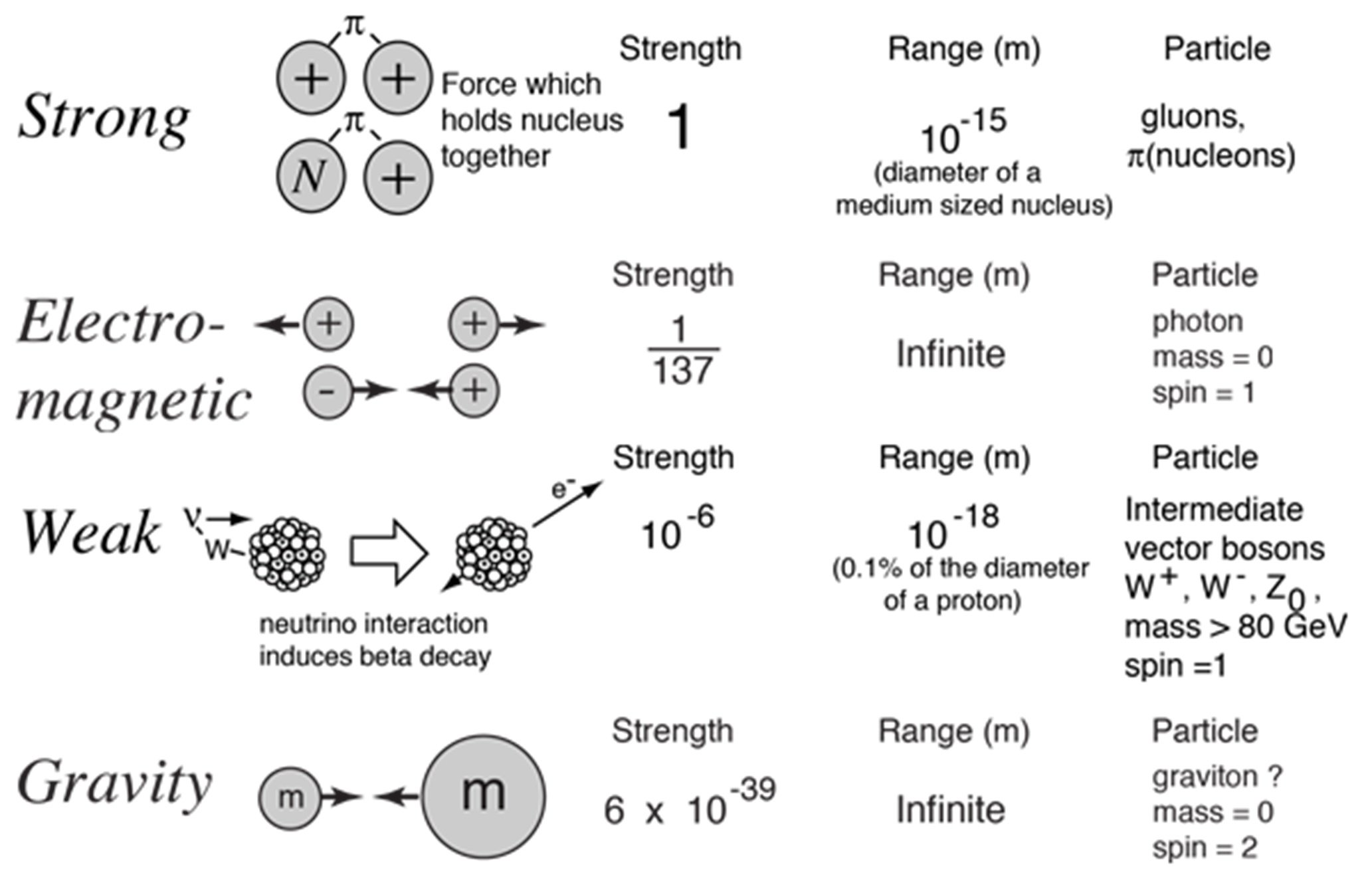
Fig. 1.3 Image Credit: Hyperphysics section for fundamental forces.#
The gravitational force (or force of mutual attraction between masses) depends on two masses (\(m_1\) and \(m_2\)), the gravitational constant \(G\), and the distance between the masses \(r\). Forces are vectors that have a magnitude and direction. Therefore, the gravitational force also has three components (one for each Cartesian direction) that are scaled by the radial direction \(\hat{r}\). Gravity follows an inverse square law and has the gravitational constant \(G = 6.6743 \times 10^{-11}\ {\rm m^3/(kg\ s^2)}\) in SI units. Mathematically, the equation for the gravitational force is given as
The electromagnetic force (or force between charges) depends on two charges (\(q_1\) and \(q_2\)), the permittivity of free space \(\epsilon_o\), and the distance between the charges \(r\). Similar to the gravitational force, it is a vector. It follows an inverse square law for the case of electrostatics and includes the cross-product for electrodynamics (see Eqn. (1.4)). The electromagnetic force is responsible for all chemical and biological processes (or practically all nongravitational forces that we experience). The electrostatic, or Coulomb, force is given by
The weak force is responsible for beta decay in nuclei, among other processes. Sheldon Glashow, Steven Weinberg, and Abdus Salam each wrote papers in the 1960s predicting that electromagnetic and weak forces were facets of the same force. They shared the Nobel Prize in 1979. Their theory also predicted the existence of new particles called \(W\) and \(Z\) bosons that were discovered in 1983. For all practical purposes, the weak interaction is effective within the nucleus and only over small distances (\(10^{-15}\ {\rm m}\)).
The strong force is the one holding the nucleus together. It is the strongest of all the forces and like the weak force, it is only effective over small distances (\(10^{-15}\ {\rm m}\)). The strong force can easily bind two protons inside a nucleus even though the Coulomb repulsion is huge. It is the strong force that allows our universe to exist through fusion process inside of stars.
1.4.2. Unification of Forces#
Physicists strive to describe nature in the most fundamental ways, where seemingly disparate forces are combined into a single force. Friction, contact, and tension forces were believed to be different forces, but today we know they are all part of the electroweak force. Around 200 years ago, the electric and magnetic forces were thought as separate, but through a series of experiments, physicists found a connection (i.e., Maxwell’s work).
Fig. 1.4 Grand unification of forces at high energies. Image Credit: OpenStax University Physics: Vol 3.#
Unification of forces remains a active area of research, where efforts are underway to unify the electroweak and strong forces through grand unified theories, or GUTs. A fashionable GUT is the mathematically complex string theory, where several predictions of GUTs have not yet been verified experimentally. As step beyond a GUT is a theory of everything (TOE), which combines all four fundamental forces (including gravity) into one theory. Figure 1.4 shows the unification of the electromagnetic and weak forces at ~100 GeV, where unification of more forces could occur at higher energies (or earlier times of the universe).
1.5. Atomic Theory of Matter#
A common idea today is that matter is composed of tiny particles called atoms, where we are told that the Greek philosophers Democritus and Leucippus proposed the concept as early as 450 B.C. The word atom comes from the Greek atomos, which means “indivisible”. However, modern physics peels back the layers of the atom, where we find that an atom is indeed divisible. This is a sign of how things change over time, where scientists were called “natural philosophers” in the past.
The theory of atoms was mostly dormant until the 17th century, where scientists were beginning to understand the properties of gases. These scientists would develop a new branch of science that we today call chemistry.
1.5.1. Developments by Chemists#
The work of Boyle, Charles, and Gay-Lussac used the idea that interactions within gases were made by tiny particles. Joseph Proust proposed the law of definite proportions that states when two or more elements combine to form a compound, the proportions by weight (or mass) of the elements are always the same.
John Dalton proposed in 1803 that the atomic theory of matter could explain the law of definite proportions if the elements are composed of atoms. Each atomic element is physically different, where the concept of atomic weights (or masses) was the key to the atomic theory.
In 1811, Avogadro proposed the existence of molecules that consist of individual or combined atoms. He stated that all gases contain the same number of molecules in equal volumes at the same temperature and pressure. Avogadro’s ideas were dismissed (rather harshly) by Dalton and others who could not imagine that atoms of the same element could combine. Stanislao Cannizzaro solved the problem of molecules in 1858 and showed how Avogadro’s ideas could be used to find atomic masses. The number of molecules in 1 gram-molecular weight of a particular element is called Avogadro’s number \(N_A\). For example, one mole of hydrogen \(({\rm H_2})\) gas has a mas of ~2 g, while one mole of carbon has a mass of about 12 g. Avogadro’s number was not even estimated until 1865.
Robert Brown observed with a microscope the motion of tiny pollen grains suspended in water, which is now called Brownian motion. The pollen appeared to move (dance) around randomly, while the water was still. Initially, the motion was ascribed to convection or organic matter, but eventually it was observed to occur for any tiny particle suspended in liquid. The explanation from atomic theory is that the molecules in the liquid are constantly pushing on the tiny grains.
1.5.2. Opposition to Atomic Theory#
The atomic theory of matter was not universally accepted, even at the end of the 19th century. Most physicists had adopted it, but there was opposition. Ernst Mach was a principal leader of the anti-atomic movement because he was an absolute positivist. His line of reasoning was that we have never seen an atom and cannot say anything about its reality. Wilhelm Ostwald supported Mach in principle. Facing difficulties in understanding radioactivity, x-rays, discrete spectral lines, and how atoms formed molecules, Ostwald contended that we should consider atoms as “hypothetical constructs”, and they were useful for bookkeeping in chemical reactions.
Max Planck grudgingly accepted the atomic theory of matter because his radiation law supported the existence of submicroscopic quanta. Boltzmann was convinced because they were necessary in his statistical mechanics.
1.5.3. Evidence for Atomic Theory#
Overwhelming evidence for the existence of atoms arrived in the first decade of the 20th century. Albert Einstein in 1905 provided an explanation of the Brownian motion observed almost 80 years earlier. Einstein explained the motion in terms of molecular motion and presented theoretical calculations for the random walk, or drunkard’s walk, problem. A random walk is a statistical process that determines how far from its initial position a tiny grain may appear after many random molecular collisions. Einstein was also able to determine the approximate mass and size of atoms and molecules from experimental data.
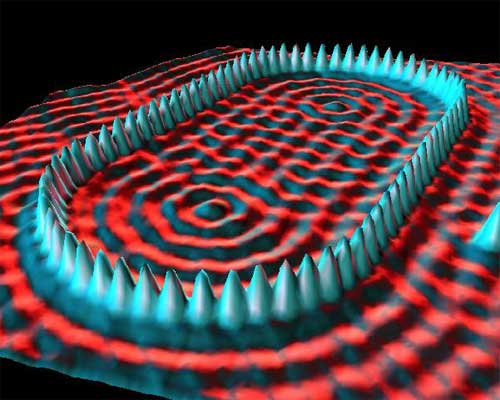
Fig. 1.5 This scanning tunneling microscope photo shows 76 individually placed iron atoms on a copper surface. The IBM researchers were trying to contain and modify electron density, observed by the wave patterns, by surrounding the electrons inside the quantum “corral.” Image Credit: Crommie, Lutz & Eigler; IBM Almaden Research Center.#
Jean Perrin presented data in 1908 from an experiment designed using kinetic theory that agreed with Einstein’s predictions. His experiment utilized four types of measurements, where each was consistent with the atomic theory and each gave a quantitative determination of Avogadro’s number. Since his experiment, the atomic theory of matter has gained nearly universal acceptance.
1.6. Unresolved Questions#
By 1895, physicists developed a good foundation for investigating nature, which includes a precise experimental method and theories that could explain many observed phenomena. The field of mechanics was in good shape, and its application let to the successes of the kinetic theory of gases and statistical thermodynamics. There was a pervasive feeling that everything could be understood by applying the techniques of experimentation and reasoning together.
However, the theory of atomic matter was not yet universally accepted and the structure of matter was unknown. Clearly, there were problems that physicists could not resolve. In 1900, Lord Kelvin referred to “two clouds on the horizon” while speaking to the Royal Institution, which were the electromagnetic medium and blackbody radiation.
1.6.1. Electromagnetic Medium#
By 1900, waves were understood by physicists to propagate within a medium. Water waves traveled in water, and sound waves could travel through any material. Therefore, electromagnetic waves need a medium to travel through, and this medium was called the luminiferous aether, or ether. By this point, experiments had deduced characteristics of the ether as
a fluid to fill space, but more rigid than steel to support the high frequencies of light waves,
massless and without viscosity, otherwise it would visibly affect the orbits of the planets,
completely transparent, non-dispersive, incompressable, and continuous at a very small scale.
Other experiments by Albert Michelson were unable to detect the ether. In 1887, Edward Morley and Michelson performed an extremely careful experiment that should have revealed the effects of the ether, which is now known as the famous Michelson-Morley experiment. Subsequent experiments by others were also negative.
1.6.2. Electrodynamics#
There was a problem of reference frames where Maxwell’s electromagnetic theory showed that an electric field in one reference system may appear as a magnetic field in another system moving relative to the first. Hertz and Lorentz were concerned that Maxwell’s equations were not invariant (keeping the same form) under a coordinate shift, or Galilean transformation. Lorentz proposed that space was contracted along the direction of motion a body, which appeared to solve the electrodynamics problem. George FitzGerald independently proposed the same concept, which led to the Lorentz-FitzGerald hypothesis in 1892.
1.6.3. Blackbody Radiation#
in 1895, thermodynamics had an interesting object called a blackbody, which absorbs the entire spectrum of electromagnetic radiation incident on it. A blackbody also emits radiation, with an emission spectrum showing the electromagnetic power emitted per unit area. Blackbody radiation was a fundamental issue because the emission spectrum is independent of the body itself.
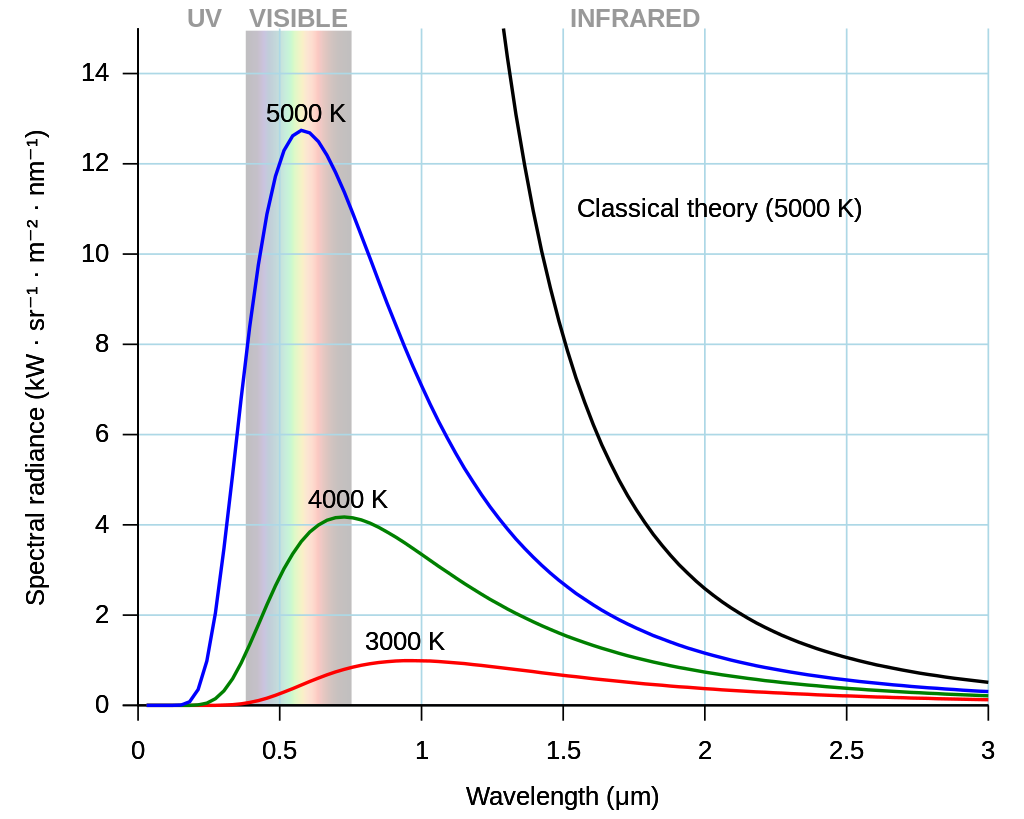
Fig. 1.6 As the temperature of a blackbody decreases, its intensity also decreases and its peak moves to longer wavelengths. Image Credit: Wikipedia; Darth Kule.#
It was possible to understand the spectrum both at the low- and high-frequency ends, separately. But, no single theory could account for the entire spectrum. The most modern theory of the day used the equipartition of energy applied to standing waves in a cavity, which resulted in an infinite emissivity (or energy density) for high frequencies, or short wavelengths. The failure of the theory was known as the “ultraviolet catastrophe.”
1.6.4. Early Discoveries (1890-1900)#
There were four discoveries that demonstrated the need for a deeper understanding of the atom.
Wilhelm Röntgen discovers x-rays in November 1895.
Henri Becquerel accidentally discovers radioactivity in February 1896 by placing uranium salt next to a carefully wrapped photographic plate. A silhouette of the uranium salt was evident, when the plate was developed.
The discovery of the electron. Faraday observed a gas discharge glow, while other scientists detected evidence of particles called cathode rays from charged cathodes. J.J. Thomson isolated a particle from the cathode ray, measured its velocity, and its ratio of charge to mass. A year earlier, Perrin proved that cathode rays were negatively charged.
Pieter Zeeman found in 1896 that a single spectral line was sometimes separated into two or three lines when the sample was placed in a magnetic field. The (normal) Zeeman effect was explained by Lorentz as the result of light begin emitted by the motion of electrons inside the atom.
In 1900, Planck completed his radiation law that solved the blackbody problem, but required that energy be quantized, or come in discrete packets. In 1905, Einstein helped solve the problem through his papers of the photoelectric effect and special relativity.
1.7. Homework Problems#
Problem 1
Summarize the major accomplishments of classical physics. How did this influence the prevailing sentiment among physicists of the 1890s?
Problem 2
Describe the developments made by chemists to characterize the behavior of gases.
Problem 3
Compare and contrast the properties of waves and particles. Which phenomena did physicists describe using either waves or particles?
Problem 5
Describe the four forces of nature and the regimes for which they act.
Problem 6
Summarize the problems that classical physics (before 1900) could not explain.


