The Theory of Special Relativity
Contents
2. The Theory of Special Relativity#
2.1. The Failure of the Galilean Transformations#
A wave is a disturbance (or energy) that flows through a medium (e.g., water waves, sound waves). James Clerk Maxwell combined the mathematical descriptions of electricity and magnetism, which together can describe light as “modulations of the same medium through which is the cause of electric and magnetic phenomena.” This insight did not precisely describe what was the medium through which light traveled.
In the late 19th century, physicists believed that light waves moved through a medium called the luminiferous aether, which is an all-pervading ether that had its roots in the science of early Greece. The ancient Greeks believed that everything was composed of five elements: earth, air, fire, water, and the ether. The ether was a more perfect element (compared to the other four) and was a major component of the crystalline spheres that held up the heavens.
There can be no doubt that the interplanetary and interstellar spaces are not empty, but are occupied by a material substance or body, which is certainly the largest, and probably the most uniform body of which we have any knowledge.
James Clerk Maxwell
Scientists of the 1800s proposed the ether for the sole purpose of transporting light waves, where an object moving through the ether would experience no mechanical resistance, so Earth’s velocity through the ether could not be directly measured. See my Modern Physics Notes for more details concerning the need for ether.
2.1.1. The Galilean Transformations#
It is impossible to tell whether you are at rest or in uniform motion (i.e., not accelerating). Galileo described a laboratory completely enclosed below the deck of a smoothly sailing ship and argued that no experiment done in this uniformly moving laboratory could measure the ship’s velocity.
Consider two inertial reference frames, \(S\) and \(S^\prime\). An inertial frame is an environment where Newton’s first law is valid:
An object at rest will remain at rest, and an object in motion will remain in motion in a straight line at constant speed, unless acted upon by an external force.
An environment consists of an infinite collection of meter stick and synchronized clocks so that the position \((x,\ y,\ \text{and}\ z)\) and time \(t\) of any event can be recorded or identified. In such a frame, there is no time delay for relaying information about an event to a distant recording device. Suppose the frame \(S^\prime\) is moving along the \(x\) direction relative to the frame \(S\) with a constant velocity \(u\). The clocks in the two frames are started when the origins \(O\) and \(O^\prime\), coincide at time \(t=t^\prime = 0\) as shown in Figure 2.1.
Fig. 2.1 The standard configuration of two frames of reference, the primed system in motion relative to the unprimed system only along the \(x\)-axis and with speed \(v\). Image Credit: Wikipedia; Krea.#
Observers in the two frames \(S\) and \(S^\prime\) measure the same moving object in terms of its position \((x,\ y,\ \text{and}\ z)\) and the time of the event \(t\) in prime and unprimed coordinates, respectively. The instantaneous measurements are related by the Galilean transformation equations:
The relationship between velocity measurements form another component to the Galilean transformation by:
Since \(u\) is a constant, its time derivative is equal to zero. As a result the measurement of acceleration (or force) is the same in both reference frames:
Thus \(\vec{F} = m\vec{a} = m\vec{a}^\prime\) for an object of mass \(m\). Newton’s laws are obey in both reference frames. No mechanical experiment can be done to measure the absolute velocity of the environment.
2.1.2. The Michelson-Morley Experiment#
Maxwell showed that electromagnetic waves move through the ether with a speed \(c\simeq 3 \times 10^8\ \rm m/s\), which seemed to open the possibility of detecting Earth’s absolute motion through the ether by measuring the speed of light from Earth’s frame of reference and comparing it to Maxwell’s theoretical value of \(c\).
In 1887, Albert A. Michelson and Edward W. Morley performed an experiment that attempted to measure the Earth’s absolute velocity. Although the Earth orbits the Sun at approximately \(30\ \rm km/s\), the results of the Michelson-Morley experiment were consistent with a velocity of Earth through the ether of zero!
Note
Strictly speaking, an environment on the Earth is not in an inertial reference frame because the Earth spins on its axis and accelerates (i.e., not constant motion) as it orbits the Sun. These noninertial effects are unimportant for the Michelson-Morley experiment.
As Earth spins on its axis and orbits the Sun, the speed of an environment should be changing as it travels through the ether. The constantly shifting ether wind should be easily detected. However, all physicists now and since have reported the same null result. Everyone measures exactly the same value for the speed of light, regardless of the velocity of the environment or the velocity of the source of the light.
Inspecting Eq. (2.2), we expect that two observers moving with a relative velocity \(u\) should obtain different values for the speed of light. The contradiction between the Galilean transformation and the experimentally determined constant speed of light means that the Galilean transformation cannot be correct in all cases. The Galilean transformations adequately describe the familiar low-speed world of everyday life (i.e., \(v\ll c\)), but they are in sharp disagreement with the experimental results involving velocities near the speed of light, \(v \sim c\). Thus, a crisis in the Newtonian paradigm was nigh.
2.2. The Lorentz Transformations#
Einstein used thought experiments or Gendankenexperiment as a tool for understanding the universe. One such discussion asked: What would you see if you looked in a mirror while moving at the speed of light? Would you see your image in the mirror or not? After much reflection, Einstein rejected the notion of the ether and developed his postulates for special relativity.
From his 1905 paper, On the Electrodynamics of Moving Bodies
The phenomena of electrodynamics as well as of mechanics posses no properties corresponding to the idea of absolute rest. They suggest rather that \(\ldots\) the same laws of electrodynamics and optics will be valid for all frames of reference for which the equations of mechanics hold good. We will raise this conjecture (the purport of which will hereafter be called the “Principle of Relativity”) to the status of a postulate, and also introduce another postulate, which is only apparently irreconcilable to the former, namely, that light is always propagated in empty space with a definite speed \(c\) which is independent of the state of motion of the emitting body.
Einstein develops two postulates as:
The Principle of Relativity: The laws of physics are the same in all inertial reference frames.
The Constancy of the Speed of Light: Light moves through a vacuum at a constant speed \(c\) that is independent of the motion of the light source.
2.2.1. The Derivation of the Lorentz Transformations#
At the heart of Einstein’s theory of special relativity are the Lorentz transformations.
Note
The Lorentz transformation equations were first derived by Hendrik A. Lorentz, but were applied to a different situation involving a reference frame at absolute rest with respect to the ether.
For the two inertial reference frames shown in Fig. 2.1, the most general set of linear transformation equation between space and time coordinates \((x,\ y,\ z,\ t)\) and \((x^\prime,\ y^\prime,\ z^\prime,\ t^\prime)\) of the same event measured from \(S\) and \(S^\prime\) are:
or
If the transformation equations were not linear, then the length of a moving object or the time interval between two events would depend on the choice of the origin for the frames \(S\) and \(S^\prime\). This is unacceptable because it would violate Einstein’s first postulate (i.e., the laws of physics cannot depend on the coordinate system).
The coefficients \(a_{ij}\) can be determined by using Einstein’s two postulates and some simple symmetry arguments. Most derivations start from using two parallel planes passing along the \(x\) direction (i.e., Fig. 2.1). There are no changes in the \(y\) or \(z\) directions between the two frames. Thus, \(y^\prime = y\) and \(z^\prime = z\), so that \(a_{22}=a_{33}=1\), whereas \(a_{21}=a_{23} = a_{24}=a_{31}=a_{32}=a_{34}=0\).
Another simplification comes from requiring that the \(t^\prime\) equation give the same result for \(\pm y\) or \(\pm z\). This must be true because rotational symmetry about the axis parallel to the relative velocity \(u\) implies that a time measurement cannot depend on the side of the \(x\) axis on which an event occurs. Thus \(a_{42} = a_{43} = 0\).
Consider the motion of the origin \(O^\prime\) of the frame \(S^\prime\). Since the frames’ clocks are synchronized at \(t=t^\prime=0\), the \(x\) coordinate of \(O^\prime\) is given by \(x=ut\) in frame \(S\) and by \(x^\prime = 0\) in frame \(S^\prime\). When \(t^\prime = 0\), then \(a_{12}=a_{13} = 0\) and \(a_{11}u = -a_{14}\). Collecting the results found thus far reveals that
If \(a_{11}=a_{44}=1\) and \(a_{41}=0\), then we would obtain the Galilean transformation. Nothing new. Now we use Einstein’s second postulate, which requires that the speed of light to be a constant. Suppose a flashbulb is set off at the common origins. At a later time \(t\) an observer in frame \(S\) will measure a spherical wavefront of light with radius \(ct\), moving away from the origin \(O\) with speed \(c\) and satisfying
Similarly, at a time \(t^\prime\), an observer in frame \(S^\prime\) will measure a spherical wavefront of light with radius \(ct^\prime\), moving away from the origin \(O^\prime\) with speed \(c\) and satisfying
Inserting the results in Eq. (2.6) into the above primed equation produces:
Comparing the coefficients for the \(x^2\) and \(t^2\) terms from the unprimed equation results in the following relations (and a bit of algebra),
Thus the Lorentz transformation equations linking the two frames \(S\) and \(S^\prime\) to the same event are:
If the inertial reference frame \(S^\prime\) is moving in the positive \(x\) direction with a velocity \(u\) relative to the frame \(S\), we get the ubiquitous factor of
called the Lorentz factor, which may be used to estimate the importance of relativistic effects. The inverse transformation equation are obtained by replacing \(u\) by \(-u\) and by exchanging the primed and unprimed quantities (i.e., \(x\rightarrow x^\prime\)).
Notice that the Lorentz transformation is approximately the Galilean transformation for \(u\ll c\) and become significantly more different as \(u / c \rightarrow 1\). The python code below produces a figure that illustrates how the relativistic factor \(\gamma\) changes with \(u / c\).
2.2.2. Four-Dimensional Spacetime#
The Lorentz transformation equations show that space and time are related (not independent of one another). Thus, they form the core of special relativity. In the words of Einstein’s professor
Henceforth space by itself, and time by itself are doomed to fade away into mere shadows, and only a kind union between the two will preserve an independent reality.
Hermann Minkowski
The physical world exists on a four dimensional spacetime, where events are identified by their spacetime coordinates \((x,\ y,\ z,\ t)\).
2.3. Time and Space in Special Relativity#
An event describes a precise location in spacetime coordinates \((x,\ y,\ z,\ t)\). Let’s suppose an observer in a frame \(S\) measures two flashbulbs going off simultaneously at a time \(t\), but at different \(x\) coordinates \(x_1\) and \(x_2\). An observer in frame \(S^\prime\) would measure the time interval \(t_1^\prime - t_2^\prime\) between the flashbulbs as
According to the observer in the \(S^\prime\) frame: if \(x_1 \neq x_2\), then the flashbulbs do not go off simultaneously because \(t_1^\prime - t_2^\prime > 0\) (for \(u>0\) and \(x_2>x_1\)). Events that occur simultaneously in one inertial reference frame do not occur simultaneously in all other inertial reference frames.
Consider one observer measures flashbulb 1 to go off after flashbulb 2. An observer moving at the same speed but in the opposite direction (\(u\rightarrow -u\)) will come to the opposite conclusion: flashbulb goes off after flashbulb 1. It is tempting to ask “Which observer is really correct?” This question is meaningless because it is equivalent to asking, “Which observer is really moving?” There is not absolute simultaneity, just as there is no absolute motion. Due to the finite speed of light, it takes time for information to flow (through photons) from one location to another.
The implications of this downfall of universal simultaneity are far-reaching. The absence of a universal simultaneity means that clocks in relative motion will not stay synchronized. Newton’s idea of an absolute universal time has been overthrown. Different observers in relative motion will measure different time intervals between the same two events!
2.3.1. Proper Time and Time Dilation#
Imagine that a strobe light located at rest relative the \(S^\prime\) frame produces a flash of light every \(\Delta t^\prime\) seconds. If one flash is emitted at time \(t_1^\prime\), then the next flash will be emitted at time \(t_2^\prime = t_1^\prime + \Delta t^\prime\) (as measured by a clock in the \(S^\prime\) frame). Using Eq. (2.11), the time interval \(\Delta t \equiv t_2 - t_1\) between the same to flashes measured by a clock in the \(S\) frame is
When \(x_2^\prime = x_1^\prime\), then the above expression becomes
This equation shows the effect of time dilation on a clock in the \(S\) frame relative to the \(S^\prime\) frame. The time interval between two events is measured differently by different observers in relative motion. The shortest time interval is measured by a clock at rest relative to to the two events, where this clock measures the proper time between the two events. Any other clock moving relative to the two events will measure a longer time interval between them.
2.3.2. Proper Length and Length Contraction#
Both time dilation and the downfall of simultaneity contradict the Newtonian notion of absolute time. The time measured between two events differs for different observers in relative motion (only noticeable when \(v\sim c\)). Since Newton believe in a separation of space and time, he also suggested that an “absolute space, in its own nature, without relation to anything external, remains always similar and immovable.” The Lorentz transformation equations require that different observers in relative motion will measure space differently as well.
Imagine a rod lies at rest relative to the \(S^\prime\) frame along the \(x^\prime\) axis. The rod’s left end is located by \(x_1^\prime\), while the right end is located by \(x_2^\prime\). Then the length of the rod is measured as \(L^\prime = x_2^\prime - x_1^\prime\) in the \(S^\prime\) frame. What is the length of the rod measured from the \(S\) frame?
Because the rod is moving relative to \(S\) (i.e., the \(S^\prime\) frame is moving relative to \(S\)), we use Eq. (2.11) to get
to measure the length in the \(S^\prime\) frame. When the measurement is take at \(t_2=t_1\), then we have
To get the length in the \(S\) frame, we simply invert the above relation to get
This equation shows the effect of length contraction on a moving rod. It says that length or distance is measured differently by two observers in relative motion. The longest length, called the rod’s proper length, is measured in the rod’s rest frame. Only lengths or distances parallel to the direction of the relative motion are affect by length contraction; distances perpendicular to the direction of the relative motion are unchanged.
2.3.3. Time Dilation and Length Contraction are Complementary#
Time dilation and length contraction are not independent effects because they come together from the Lorentz transformation equations. They are complementary, where the magnitude of either effect depends on the motion of the event begin observed relative to the observer.
Exercise 2.1
Cosmic rays from space collide with the nuclei from atoms in Earth’s upper atmosphere, producing elementary particles called muons. Muons are unstable and decay after an average lifetime \(\tau=2.20\ \rm \mu s\), as measured in a laboratory where the muons are at rest. The number of muons in a given sample should decrease with time according to \(N(t) = N_o e^{-t/\tau}\), where \(N_o\) is the original number of muons in the sample at \(t=0\). At the top of Mt. Washington (\(1907\ \rm m\) above sea level in New Hampshire), a detector counted \(563\ \rm muons/hr\) moving downward at a speed \(u = 0.9952c\).
How many muons per hour would be counted at sea level?
Naively, we might find the time-of-flight \(t\) for the muons to get from the top of the mountain to the ground using \(t=L/u\), and substitute the time-of-flight into the equation for exponential decay to get
A muon detector at sea level measures \(\text{408 muons/hr}\), which shows that our naive calculation is incorrect. The muons are moving near the speed of light and thus must be treated relativistically.
The distance from the mountain top to sea level is contracted and the decay timescale is dilated due to special relativity. The difference between these two effects depends on the assumed reference frame: mountain or muon.
From a muon’s rest frame it’s lifetime is only \(2.20\ \rm \mu s\), where an observer riding along with the muon would measure a severely-contracted Mt. Washington in the direction of motion. The distance traveled \(L^\prime\), time-of-flight \(t^\prime\), and measured number of muons/hr would be
Alternatively, the experimenters clocks on Mt. Washington are moving relative to the muons, which means they will measure a longer (dilated) lifetime \(\tau^\prime\). After correcting for the dilated lifetime, we can follow the naive calculation to get
Note that the relativistic muon lifetime is more than ten times the muon’s lifetime when measured in its own rest frame. The moving muons’ clocks run slower, so more of them survive long enough to reach sea level.
Both methods (length contraction and time dilation) give good agreement with the measured value at sea level. Moreover, they agree with each other, which shows that an effect due to time dilation as measured in one frame may instead be attributed to length contraction as measured in another frame.
from scipy.constants import c
import numpy as np
N_o = 563. #muons per hr
tau = 2.2e-6 #average muon lifetime in sec
u = 0.9952*c #speed of muons on Mt. Washington
L = 1907 #height of Mt. Washington above sea level in m
#First approach using t = L/u
t = L/u
N = N_o*np.exp(-t/tau)
print("The expected number of muons/hr (Netwonian) at sea level is %i." % np.round(N,0))
#Relativistic approach using gamma factor and length contraction
gamma = 1./np.sqrt(1-u**2/c**2)
L_prime = L/gamma
t_prime = L_prime/u
N = N_o*np.exp(-t_prime/tau)
print("The contracted distance is %3.1f m." % L_prime)
print("The expected number of muons/hr (relativistically) at sea level is %i." % np.round(N,0))
#Relativistic approach using gamma factor and time dilation
tau_prime = gamma*tau
t = L/u
N = N_o*np.exp(-t/tau_prime)
print("The dilated time is %2.2f microsec." % np.round((t/1e-6),2))
print("The expected number of muons/hr (relativistically) at sea level is %i." % np.round(N,0))
The expected number of muons/hr (Netwonian) at sea level is 31.
The contracted distance is 186.6 m.
The expected number of muons/hr (relativistically) at sea level is 424.
The dilated time is 6.39 microsec.
The expected number of muons/hr (relativistically) at sea level is 424.
2.3.4. The Relativistic Doppler Shift#
In 1842 Christian Doppler showed that as a source of sound moves through a medium (e.g., air), the wavelength is compressed in the forward direction and expanded in the backward direction. This change in wavelength of any type of wave caused by the motion of the source or the observer is called Doppler shift.
Doppler deduced that the difference between the observed wavelength \(\lambda_{\rm obs}\) for a moving source of sound and the rest wavelength \(\lambda_{\rm rest}\) measured in the laboratory for a reference source is related to the radial velocity \(v_r\) (i.e., the component of velocity directly toward or away from the observer) by
where \(v_s\) is the speed of sound in the medium. However, this expression cannot be precisely correct for light. The Doppler shift for light is a qualitatively different phenomenon from its counterpart for sound waves.
Consider a distant light source that emits a light signal at time \(t_1\) and another signal at time \(t_2 = t_1 + \Delta t\) as measured by a clock at rest relative to the source. If this light source is moving relative to an observer with a velocity u, then the time-of-flight and the distance traveled by the light signals will be different. The time between the emission of the light signals as measured in the observer’s frame is
In this time, the observer determines that the distance to the light source has changed by an amount
Thus the time interval \(\Delta t_{\rm obs}\) between the arrival of the two light signals at the observer’s location is
If \(\Delta t\) is the time between the emission of the light wave crests and \(\Delta t_{\rm obs}\) is the time between their arrival, then the frequencies of the light wave are \(\nu_{\rm rest} = 1/\Delta t\) and \(\nu_{\rm obs}= 1/\Delta t_{\rm obs}\). The equation describing the relativistic Doppler shift is
where \(v_r = u\cos{\theta}\) is the radial velocity of the light source. If the light source is moving directly away or toward the observer, then the angle \(\theta\) is \(0^\circ\) or \(180^\circ\), respectively. The relativistic Doppler shift reduces to
There is also a transverse Doppler shift for perpendicular motion relative to the observer’s line-of-sight (i.e., \(\theta = 90^\circ\)). This transverse shift is entirely due to time dilation.
When astronomers observe a star or galaxy moving away from or toward Earth, the wavelength of the light they receive is shifted toward longer or shorter wavelengths, respectively.
If the source of light is moving away from the observer \((v_r>0)\), then \(\lambda_{\rm obs} > \lambda_{\rm rest}\). This shift to a longer wavelength is called a redshift.
Similarly, if the source is moving toward the observer \((v_r<0)\), then there is a shift to a shorter wavelength, or a blueshift.
Because most of the objects in the universe outside of our own Milky Way Galaxy are moving away from us, redshifts are more commonly measured. A redshift parameter \(z\) is used to describe the change in wavelength and is defined as
Using the relativistic frequency \(\nu_{\rm obs}/\nu_{\rm rest}\) for radial motion and \(c = \lambda \nu\), we get
and the redshift parameter becomes
Alternative forms of the redshift parameter are:
If the luminosity of an astrophysical source with redshift parameter \(z>0\) (receding) is observed to vary during a time \(\Delta t_{\rm obs}\), then the change in luminosity occurred over a shorter time \(\Delta t_{\rm rest} = \Delta t_{\rm obs}/(z+1)\) in the rest frame of the source.
Exercise 2.2
In its rest frame, the quasar SDSS 1030+0524 produces a hydrogen emission line of wavelength \(\lambda_{\rm rest} = 121.6\ \rm nm\). On Earth, this emission line is observed to have a wavelength of \(\lambda_{\rm obs} = 885.2\ \rm nm\).
What is the redshift parameter \(z\) and radial velocity \(v_r\) for this quasar?
The redshift parameter can be determined through the ratio of the difference in wavelengths to the rest wavelength. Quantitatively, this is given by
The redshift parameter is needed to determine the radial velocity. Using Eq. (2.25), we may calculate the recessional speed of the quasar by
which results in \(v_r = 0.963c.\)
Quasar SDSS 1030+0524 appears to moving away from us at \(>96\%\) of the speed of light! However, the overall expansion of the universe contributes to large recessional speeds for objects that are very far away from us. In these cases, the increase in the observed wavelength is actually due to the expansion of space itself rather than being due to the motion of the object through space! This is known as cosmological redshift and is a consequence of the Big Bang.*
lambda_rest = 121.6 #rest wavelength in nm
lambda_obs = 885.2 #observed wavelength in nm
#Calculation of z parameter
z = (lambda_obs-lambda_rest)/lambda_rest
print("The redshift parameter is %1.2f." % z)
#Calculation of radial velocity (in units of c)
v_r = ((z+1)**2 - 1)/((z+1)**2 + 1)
print("The recessional velocity is %1.3f c." % v_r)
The redshift parameter is 6.28.
The recessional velocity is 0.963 c.
Suppose the speed u of a light source is small compared to the speed of light (i.e., \(u/c\ll 1\)). We can evaluate \((1+v_r/c)\) terms in the equation for the redshift parameter \(z\) (Eq. (2.25)). This binomial approximation produces
Applying the above approximations to the redshift parameter equation gives
Since \(v_r/c \ll 1\), then \(1-v_r/(2c) \approx 1\). At low speeds, we can obtain
where \(v_r > 0\) for a receding source (and vice versa for an approaching source). Although this equation is similar to the equation derived by Doppler, you should remember that it is an approximation, valid only for low speeds. Misapplying this equation to the relativistic qusaar SDSS 1030+0524 would lead to the erroneous conclusion that the quasar is moving away from us at \(6.28\) times the speed of light!
2.3.5. The Relativistic Velocity Transformation#
Because space and time intervals are measured differently by different observers in relative motion, velocities must be transformed as well. The equations describing the relativistic transformation of velocities may be easily found from the Lorentz transformation equations (Eq. (2.11)) by writing them as differentials:
Then dividing the \(dx^\prime\), \(dy^\prime\), and \(dz^\prime\) equations by the \(dt^\prime\) equation to get:
As with the inverse Lorentz transformations, the inverse velocity transformations may be obtained switching primed and unprimed quantities and by \(u\rightarrow -u\).
Exercise 2.3
As measured in the \(S^\prime\) reference frame, a light source is at rest and radiates equally in all directions. In particular, half of the light is emitted into the forward (\(x^\prime>0\)) hemisphere.
Is the situation any different when viewed from the \(S\) reference frame?
In the \(S\) frame, the light source is traveling in the \(x>0\) direction with a relativistic speed \(u\). Consider the velocity components of a light ray in the \(S^\prime\) frame as
This light ray travels along the boundary between the forward and backward hemispheres of light measured in the \(S^\prime\) frame. However, as measured in the \(S\) frame, this light ray has the velocity components given by the inverse transformation of the velocity Lorentz transformation, or
In the \(S\) frame, the light ray has a \(v_y\) component and is not traveling perpendicular to the \(x\) axis. In fact, for \(u/c \sim 1\), the angle \(\theta\) measured by the light ray and the \(x\) axis may be found from \(\sin{\theta} = v_y/v\), where
is the speed of the light ray measured in the \(S\) frame. Thus
where \(\gamma\) is the Lorentz factor. For relativistic speeds \(u \approx c\), which implies that \(\gamma\) is large and \(\sin{\theta}\) becomes very small. All of the light emitted into the forward hemisphere is concentrated into a narrow cone in the direction of the light source’s motion when measured in the \(S\) frame. This is called the headlight effect and plays an important role in many areas of astrophysics. For example, as relativistic electron spiral around magnetic field lines, they emit synchrotron radiation. This radiation is concentrated in the direction of the electron’s motion and is strongly plane-polarized. Synchrotron radiation is an important electromagnetic radiation process in the Sun, Jupiter’s magnetosphere, pulsars, and active galaxies.
2.4. Relativistic Momentum and Energy#
Up to this point, the position and velocities are transformed through the Lorentz transformation. Einstein’s theory of special relativity incorporates these ideas to transform the concepts of momentum and energy. According to the Principle of Relativity, if momentum is conserved in one inertial frame of reference, then it must be conserved in all inertial frames. This leads to a definition of the relativistic momentum vector p:
where \(\gamma\) is the Lorentz factor.
Note
The mass \(m\) of a particle is taken to be the same value in all inertial reference frames. Thus, the mass of a moving particle does not increase with increasing speed, although its momentum approaches infinity as \(v \rightarrow c\). Also note that the \(v\) in the denominator is the magnitude of the particle’s velocity relative to the observer, not the relative velocity \(u\) between two reference frames.
2.4.1. The Derivation of \(E=mc^2\)#
Using Eq. (2.31) and the relation for the kinetic energy (e.g., \(K = p^2/2m\)), we can derive an expression for the relativistic kinetic energy.
Starting with Newton’s second law (\(\mathbf{F} = d\mathbf{p}/dt\)) applied to a particle of mass \(m\) that is initially at rest. Consider a force of magnitude \(F\) that acts on the particle in the \(x\) direction. The particle’s final kinetic energy \(K\) equals the total work done by the force on the particle as it travels from its initial position \(x_i\) to its final position \(x_f\):
where \(p_i\) and \(p_f\) are the initial and final momenta of the particle, respectively. Integrating by parts using the initial condition \(p_i = 0\) gives
If we drop the \(f\) in the subscript, the expression for the relativistic kinetic energy becomes
The right-hand side of the expression for the kinetic energy consists of the difference between two energy terms. The first is identified as the total relativistic energy \(E\),
The second term is an energy that does not depend on the speed of the particle. The particle has this energy at rest, and thus, it is called the rest energy of the particle:
The particle’s kinetic energy is its total energy minus its rest energy. When the energy of a particle is given (e.g., \(40\ \rm MeV\)), the implicit meaning is that it refers to the particle’s kinetic energy, where the rest energy is not included.
A very useful expression relates a particle’s total energy \(E\), the magnitude of its momentum \(p\), and its rest energy \(mc^2\), which is
The above equation is valid even for particles with no mass (e.g., photons).
For a system of \(n\) particles, the total energy \(E_{\rm sys}\) is the sum of the total energies \(E_i\) of the individual particles:
Similarly, the vector momentum \(\mathbf{p}_{\rm sys}\) is the sum of the momenta \(\mathbf{p}_i\) of the individual particles:
If the momentum of the system of particles is conserved, then the total energy is also conserved, even for inelastic collisions in which the kinetic energy of the system:
is reduced. The kinetic energy lost in the inelastic collisions goes into increasing the rest energy, and hence the mass of the particles. This increase in energy allows the total energy of the system to be conserved. Mass and energy are two sides of the same coin; one can be transformed into the other.
Exercise 2.4
In a one-dimensional completely inelastic collision, two identical particles of mass \(m\) and speed \(v\) approach each other, collide head-on, and merge to form a particle of mass \(M\).
Show how the lost kinetic energy is transformed into mass relativistically.
The initial energy of the system of particles is
Since the initial momenta of the particles are equal in magnitude and opposite in direction the momentum of the system \(\mathbf{p}_{\rm sys} = 0\) before and after the collision. Thus after the collision, the particle is at rest and its final energy is
Equating the initial and final system energies shows that the mass \(M\) of the conglomerate particle is
Thus the particle mass has increased by an amount:
The origin of this mass increase is found by comparing the initial and final values of the kinetic energy. The initial kinetic energy of the system is
and the final kinetic energy \(K_{{\rm sys},f} = 0.\) Dividing the kinetic energy lost in this inelastic collision by \(c^2\) equals the particle mass increase, \(\Delta m\).
2.4.2. The Derivation of Relativistic Momentum#
For the relativistic momentum, let’s consider a glancing elastic collision between two identical particles of mass \(m\). This collision can be observed from three carefully chosen inertial reference frames (\(S\), \(S^\prime\), and \(S^{\prime\prime}\)) as shown in Figure 2.2.
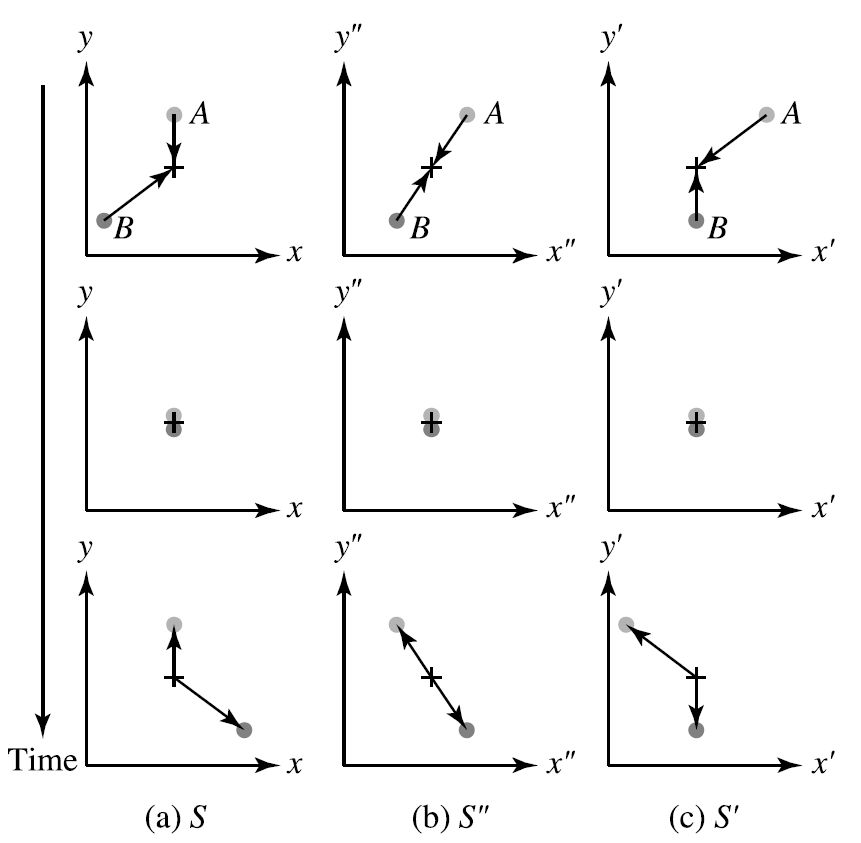
Fig. 2.2 An elastic collision measured in frames (a) \(S\), (b) \(S^{\prime\prime}\), and (c) \(S^{\prime}\). As observed from the \(S^{\prime\prime}\) frame, the \(S\) frame moves in the negative \(x^{\prime\prime}\) direction, along with particle \(A\), and the \(S^\prime\) frame moves in the positive \(x^{\prime \prime}\) direction, along with particle \(B\). For each reference frame, a vertical sequence of three figures shows the situation before (top), during, and after the collision. Figure credit: Carroll & Ostlie (2007).#
When measured in the inertial \(S^{\prime\prime}\) frame, the two particles \(A\) and \(B\) have velocities and momenta that are equal in magnitude and opposite in direction before and after the collision (i.e., momentum is conserved).
If the \(S\) frame moves in the negative \(x^{\prime\prime}\) direction with a velocity equal to the \(x^{\prime\prime}\) component of particle \(A\) in the \(S^{\prime\prime}\) frame, then the velocity of particle \(A\) has only a \(y\) component in the \(S\) frame.
Similarly, if \(S^\prime\) moves in the positive \(x^{\prime\prime}\) direction with a velocity equal to the \(x^{\prime\prime}\) component of particle \(B\) in the \(S^{\prime\prime}\) frame, then the velocity of particle \(B\) has only a \(y\) component.
This means that the change in the \(y\) component of particle \(A\)’s momentum as measured in the \(S\) frame is the same as the change in the \(y^\prime\) component of particle \(B\)’s momentum as measured in the \(S^\prime\) frame, except for a change in sign: \(\Delta p_{A,y} = -\Delta p^\prime_{B,y}\).
The momentum must be conserved in the \(S\) and \(S^\prime\) frames, just as it is in the \(S^{\prime\prime}\) frame. This means that in the \(S^\prime\) frame, the sum of the changes in the \(y^\prime\) components of particle \(A\)’s and \(B\)’s momenta must be zero: $\Delta p^\prime_{A,y} + \Delta p^\prime_{B,y} = 0. Combining these results gives
So far, the argument has been independent of a specific formula for the relativistic momentum vector \(\mathbf{p}\). Let’s make a couple of assumptions.
The relativistic momentum vector has the form: \(\mathbf{p} = fm\mathbf{v}\), where \(f\) is a relativistic factor that depends on the magnitude of the particle’s velocity, but not its direction.
The \(y\) and \(y^\prime\) components of each particle’s velocity are chose to be arbitrarily small compared to the speed of light \(c\).
The \(y\) and \(y^\prime\) components of particle \(A\)’s velocity are extremely small and the \(x^\prime\) component of particle \(A\)’s velocity is taken to be relativistic. Since
in the \(S^\prime\) frame, the relativistic factor \(f^\prime\) for particle \(A\) in the \(S^\prime\) frame is not equal to 1, whereas \(f\) is arbitrarily close to unity in the \(S\) frame. If \(v_{A,y}\) is the final \(y\) component of particle \(A\)’s velocity, and similarly for \(v^\prime_{A,y}\), then Eq. (2.36) becomes
The relative velocity \(u\) of frames \(S\) and \(S^\prime\) is needed to relate \(v^\prime_{A,y}\) and \(v_{A,y}\) using Eq. (2.29).
\(v_{A,x} = 0\) in the \(S\) frame, so \(u=v^\prime_{A,x}\).
\(v^\prime_{A,y}\) is arbitrarily small, we can set \(v^\prime_{A,x} = v^\prime_A = u\)
From Eq. (2.29) for the \(y\) component we get
Inserting this relation into Eq. (2.37) reveals the relativistic factor \(f\) to be
as measured in the \(S^\prime\) frame. Dropping the prime superscript and the \(A\) subscript gives
The formula for the relativistic momentum vector is thus
which is equivalent to Eq. (2.31).
2.5. Homework#
Problem 1
A rod moving relative to an observer is measured to have its length \(L\) contracted to one-half of its length when measured at rest. Find the value of \(u/c\) for the rod’s rest frame relative to the observer’s frame of reference.
Problem 2
An astronaut in a starship travels to \(\alpha\) Centauri (\(4.367\ \rm ly\) away from Earth) at a speed of \(u = 0.8c\).
(a) How long does the trip to \(\alpha\) Centauri take, as measured by a clock on Earth?
(b) How long does the trip to \(\alpha\) Centauri take, as measured by the starship pilot?
(c) What is the distance between Earth and \(\alpha\) Centauri, as measured by the starship pilot?
(d) A radio signal is sent from Earth to the starship every 6 months, as measured bya clock on Earth. What is the time interval between the reception of one of these signals and reception of the next signal aboard the starship?
(e) A radio signal is sent from the starship to the Earth every 6 months, as measured bya clock aboard the starship. What is the time interval between the reception of one of these signals and reception of the next signal on Earth?
(f) If the wavelength of the radio signal sent from Earth is \(\lambda = 15\ \rm cm\), to what wavelength must the starship’s receiver be tuned?
Problem 3
In its rest frame, quasar Q2204+29 produce a hydrogen emission line of wavelength \(121.6\ \rm nm\). Astronomers on Earth measure a wavelength of \(656.8\ \rm nm\) for this line. Determine the redshift parameter and the apparent speed of recession for this quasar. (For more information about this quasar, see McCarthy et al. 1988)
Problem 4
Starship A moves away from Earth with a speed of \(v_A = 0.8c\). Starship B moves away from Earth in the opposite direction with a speed of \(v_B = 0.6c\).
(a) What is the speed of starship A as measured by starship B?
(b) What is the speed of starship B as measured by starship A?

