5. Free and Forced Eccentricity

Planets can experience a small but coherent forcing over time, which is referred to as a secular perturbation. This type of forcing is reminiscent of perturbations of a harmonic oscillator or pendulum.

Consider a pendulum (or swing) that oscillates back and forth. If the perturbation (even if small) is timed when the pendulum reaches its maximum height and along the natural direction of motion, then the overall amplitude of the oscillation will increase over time because the pendulum is receiving a coherent boost along the direction of motion.

This is in contrast to the pendulum receiving a boost randomly along and against the direction of motion. If the direction and magnitude of the kicks are truly random, then the boost in each direction should cancel out on average resulting in no growth in the oscillation amplitude.

The components of free and forced eccentricity are described mathematically using concepts of forced and free oscillations of harmonic oscillators that are connected together. This is similar to the problem of a damped, driven oscillator, which has a linear combination of a steady-state and transient solution. The steady-state solution maps to the forced eccentricity, where the transient solution is the free eccentricity. The following section reviews the physics of coupled oscillations.

5.1. A review of coupled oscillations

Consider two masses on a frictionless plane, where each mass is connected by a spring (with a spring constant \(k\)) to a wall. Each spring experiences a force according to Hooke’s law (e.g., \(F = -kx\)). Additionally, the two springs are connected to one another by another spring with a spring constant \(\kappa\).

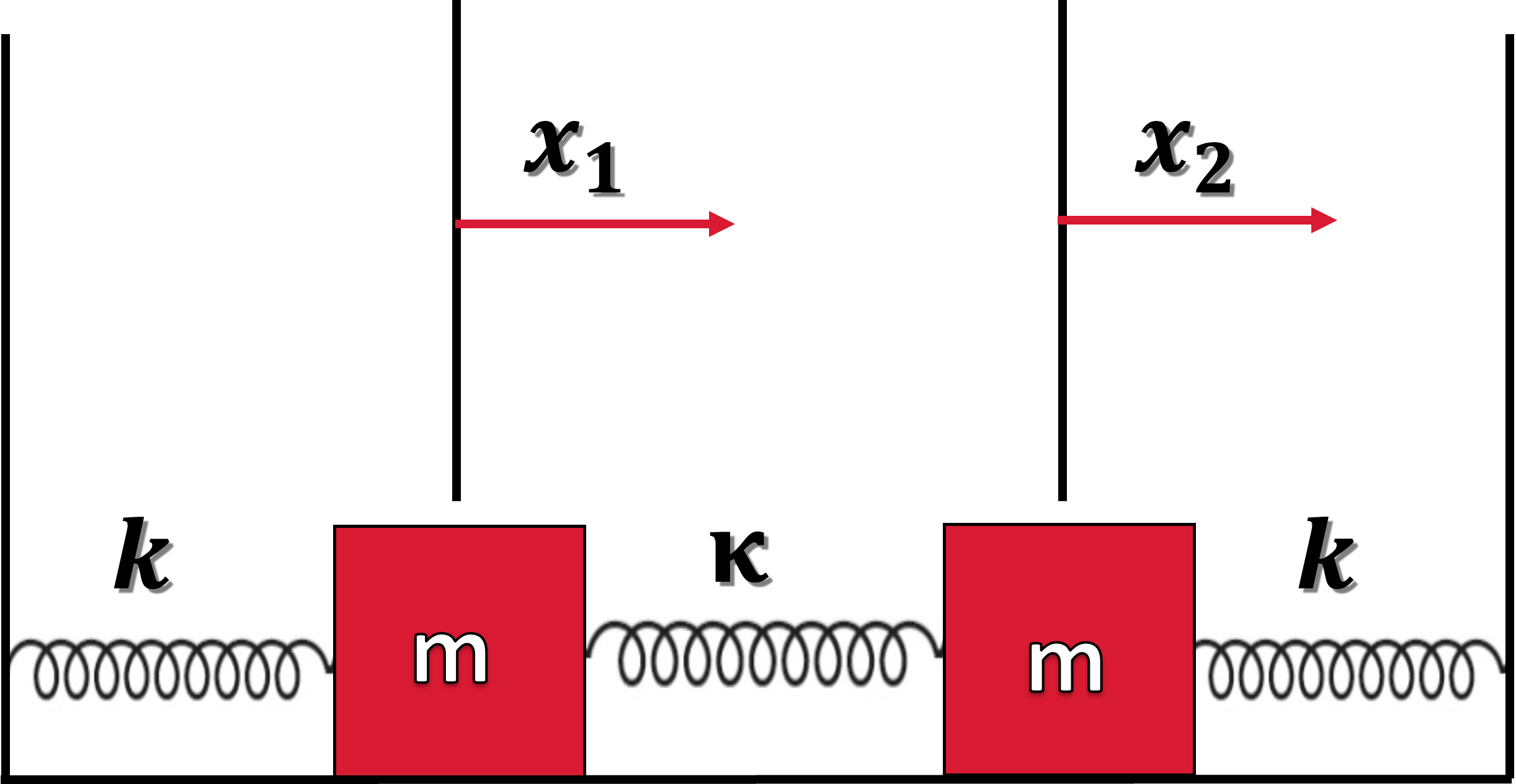
Fig. 5.1 Two identical masses attached to their respective wall with a spring with a spring constant \(k\). The masses are coupled by another spring (with a spring constant \(\kappa\)) and slide on a frictionless plane.

The mass on the left is displaced by a distance \(x_1\) to the right. It’s left spring will apply a force to bring it back to the equilibrium, but the middle spring will compress along with the rightmost spring. The compression of the middle and right spring will apply a force on the other mass on the right. Because the masses are connected, there will be a similar set of forces acting on the mass on the right. Altogether the forces on the left and right mass are:

(5.1)\[\begin{align} \mathbf{F}_{\rm left} &= -kx_1 + \kappa(x_2-x_1) = m\ddot{x}_1, \\ \mathbf{F}_{\rm right} &= -kx_2 + \kappa(x_1-x_2) = m\ddot{x}_2. \end{align}\]

Notice that each of these equations have a part that we expect from an isolated spring and a part that describes the interaction via the connecting spring with spring constant \(\kappa\). Furthermore, the interaction on the left mass is equal and opposite to the interaction force on the right mass. The above equations can be rearranged to get:

(5.2)\[\begin{align} m \ddot{x}_1 &= -(\kappa + k)x_1 + \kappa x_2, \\ m \ddot{x}_2 &= \kappa x_1 - (\kappa + k)x_2, \end{align}\]

or in matrix form as:

(5.3)\[\begin{align} \begin{pmatrix} m\ddot{x}_1 \\ m\ddot{x}_2 \end{pmatrix} &= \begin{bmatrix} -(\kappa + k) & \kappa \\ \kappa & -(\kappa + k) \end{bmatrix} \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}. \end{align}\]

Let’s use the following trial functions:

(5.4)\[\begin{align} x_1(t) &= B_1 e^{i\omega t}, \\ x_2(t) &= B_2 e^{i\omega t}, \end{align}\]

based on our prior knowledge concerning the isolated springs. Upon substitution, we get

(5.5)\[\begin{align} -m\omega^2\begin{pmatrix} B_1 e^{i\omega t} \\ B_2 e^{i\omega t} \end{pmatrix} &= \begin{bmatrix} -(\kappa + k) & \kappa \\ \kappa & -(\kappa + k) \end{bmatrix} \begin{pmatrix} B_1 e^{i\omega t} \\ B_2 e^{i\omega t} \end{pmatrix}, \end{align}\]

or

(5.6)\[\begin{align} \begin{bmatrix} (\kappa + k) - m\omega^2 & -\kappa \\ -\kappa & (\kappa + k) - m\omega^2 \end{bmatrix} \begin{pmatrix} B_1 e^{i\omega t} \\ B_2 e^{i\omega t} \end{pmatrix} &= \begin{pmatrix} 0 \\ 0 \end{pmatrix}. \end{align}\]

The trivial solution is \(B_1 = B_2 = 0\). But the non-trivial solution is solved via the characteristic equation (or determinant) via:

(5.7)\[\begin{align} \left[(\kappa + k) - m\omega^2\right]^2 - \kappa^2 &= 0, \\ (m\omega^2)^2 - 2m(\kappa + k)\omega^2 + (\kappa + k)^2 - \kappa^2 &= 0, \\ x^2 -2(\kappa+k)x + 2\kappa k + k^2 & = 0, \end{align}\]

which has solutions via the quadratic equation:

(5.8)\[\begin{align} x &= (\kappa + k) \pm \frac{1}{2}\sqrt{4(\kappa + k)^2 - 4(2\kappa k + k^2)}, \\ m\omega^2 &= (\kappa + k) \pm \kappa, \\ \omega &= \pm \sqrt{\frac{(\kappa + k) \pm \kappa}{m}}. \end{align}\]

Each root (from the quadratic equation) permits a separate eigenfrequency:

(5.9)\[\begin{align} \omega_1 = \pm \sqrt{\frac{2\kappa + k}{m}}, \qquad& \text{and} \qquad& \omega_2 = \pm \sqrt{\frac{k}{m}}. \end{align}\]

To determine the coefficients \(B_1\) and \(B_2\), we substitute the eigenfrequencies (\(\omega_1\) and \(\omega_2\)) back into the characteristic equation to get:

(5.10)\[\begin{align} \left[ k + \kappa - (k + 2\kappa) \right]B_1 - \kappa B_2 &= -\kappa (B_1 + B_2) = 0,&\ (\text{for } \omega_1;\ B_1 = -B_2) \\ \left( k+ \kappa - k\right)B_1 - \kappa B_2 &= \kappa (B_1 - B_2) = 0.& (\text{for } \omega_2;\ B_1 = B_2) \end{align}\]

The most general solution of the coupled harmonic oscillator problem is

(5.11)\[\begin{align} x_1(t) &= B_1^+ e^{+i\omega_1 t} + B_1^- e^{-i\omega_1 t} + B_2^+ e^{+i\omega_2 t} + B_2^- e^{-i\omega_2 t}, \\ x_2(t) &= -B_1^+ e^{+i\omega_1 t} - B_1^- e^{-i\omega_1 t} + B_2^+ e^{+i\omega_2 t} + B_2^- e^{-i\omega_2 t}. \end{align}\]

Depending on initial and boundary conditions, Euler’s equation could be used to transform the above into a linear combination of \(\sin\) and \(\cos\) functions. For more details, see the lecture by Matthew Schwartz at Harvard or libretexts by Tom Weideman at UC Davis, or lectures on YouTube from Jeffery Chasnov (see below). There is also a guide for the generalized method from Lagrangian dynamics provided by the University of Rochester that may be helpful.

5.2. Impact of forced eccentricity

5.3. Minimizing the forced eccentricity

5.4. A sample simulation