2. Patterns in the Sky#
2.1. How to estimate Earth’s Size#
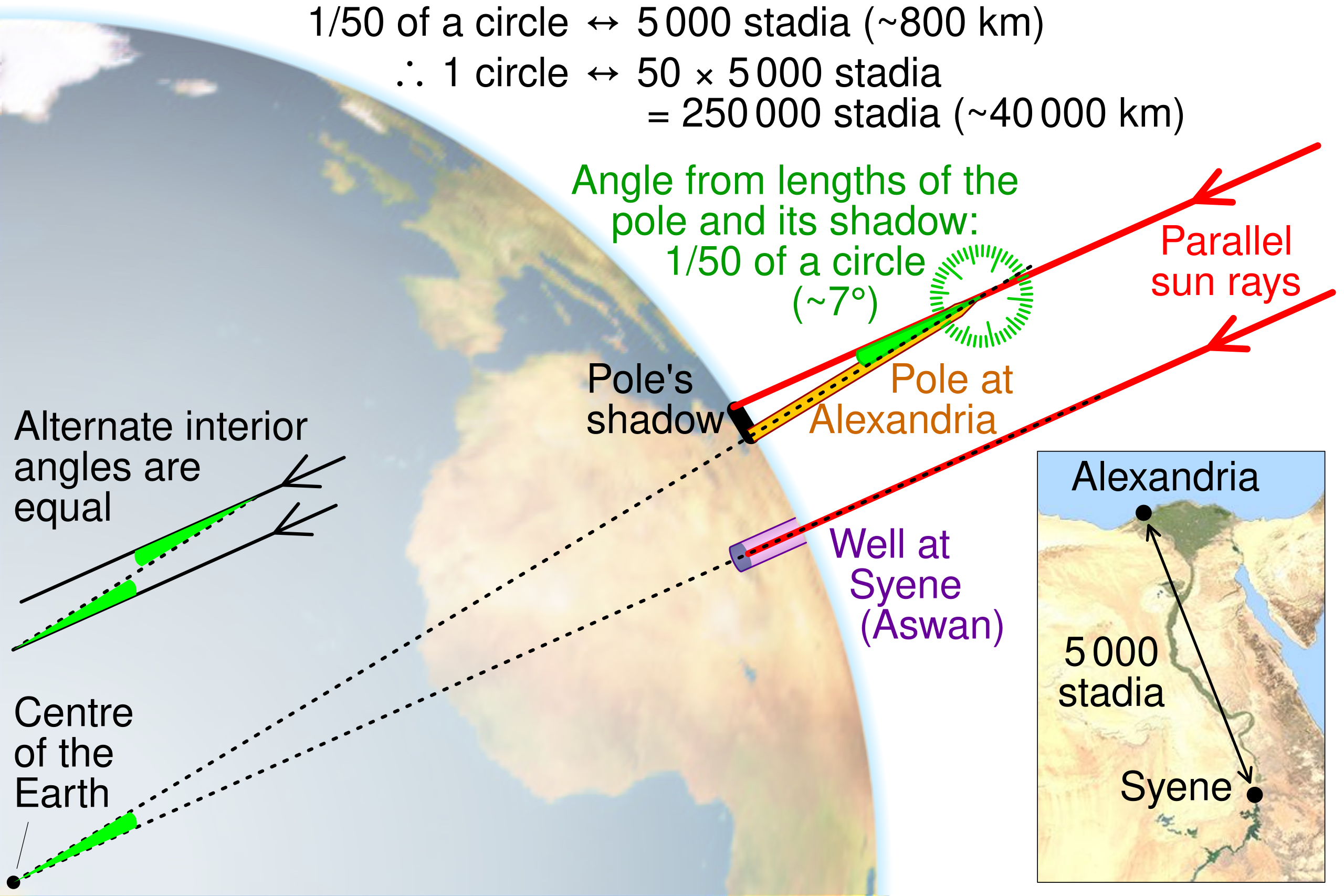
In \({\sim}230\) BC, a Greek astronomer named Erathosthenes performed an experiment to measure the circumference of the Earth. He had come across an account in the library at Alexandria that on the summer solstice (~June 21) a well in Syene (now Aswan) cast no shadow. This observation was peculiar because the many columns in Alexandria did cast shadows on the very same day.
During Eratosthenes time, it was already known (or at least presumed) that the Earth was a sphere. This is apparent through:
the use of the celestial sphere for astronomical observations, or
walking due south to see buildings fall below the horizon, or
watching ships sail away and fall below the horizon.
These observations are explained by a spherical Earth. However, it was not known how big the Earth actually is or the distance around the Earth.
Eratosthenes assumed that the Sun was really far away, or at least far away enough that individual light rays from the Sun arrived at Earth’s surface in parallel. As a result, he could use basic geometry and trigonometry to determine the circumference of the Earth. The diagram below illustrates that the angle \(\theta\) the Sun’s rays makes with a column in Alexandria to cast the shadow would be the same angle subtended by the distance between Alexandria and Syene.
First, Eratosthenes needed to measure the angle \(\theta\). This can easily be done by measuring the shadow length \(s\) along the ground in Alexandria and the column height \(h\). The angle \(\theta\) is then given by:
Note that this calculation is simplified because no shadow is cast at Syene. If both locations had shadows, shadow lengths and column heigts would be measured at both locations to obtain a \(\theta_1\) and \(\theta_2\) corresponding to each location. Then, the angle \(\theta\) would be the difference between the two angles (if along the same longitude), or \(\theta = |\theta_1-\theta_2|\).
Next, Eratosthenes needed to measure the distance \(d\) from Alexandria to Syene. This was accomplished by simply hiring someone to walk out (measure) the distance, observe that the account in Syene was correct, and walk back. Eratosthenes determined that \(\theta \approx 7^\circ\) and \(d = 5000\ {\rm stadia}\) (singular: stadion). Accounts vary on how big a stadion was, where for this example we assume that it is \(160\ {\rm m/stadion}\).
With the above values Eratosthenes measured the circumference \(C\) by
The actual circumference of Earth is \({\sim}40,075\ {\rm km}\). Eratosthenes’ measurement was only a few percent from the true value!
2.1.1. Modern day experiments#
Undergraduates can perform this experiment with relative ease, but getting a similar accuracy can still be a little tricky. The video below (from Dr. David Sederberg at Purdue) shows several ways to construct a vertical column, or gnomon. But, you will need a collaborator at a different location (preferably same longitude) to take the measurement simultaneosly.
Valdosta State University (in Valdosta, Georgia) and Henry Ford College (in Dearborn, Michigan) conducted this experiment in Spring 2022 (and several subsequent semesters). Here are some of their results.
The measurement at Valdosta State used a gnomon that was \(94.3\ {\rm cm}\) tall, which measured a shadow length of \(35.8\ {\rm cm}\). The angle \(\theta_1\) at Valdosta State was \(20.8^\circ\) Below is a video showing the measurement.
The measurement at Henry Ford College used a meter stick as the gnomon (\(100\ {\rm cm}\)), which measured a shadow length of \(65.2\ {\rm cm}\). The angle \(\theta_2\) at Henry Ford College was \(33.1^\circ\).

With these measurements and the distance between the two locations (\(d = 1276\ {\rm km}\) as the crow flies), they made an estimate for Earth’s circumference.
The experiment produced a 7% error when compared to the actual value, but it was the very first try. Subsequent semesters obtained values much closer to the actual circumference with only ~2% error.