2. Python Basics#
2.1. What is Python?#
Python is an interpreted high-level programming language that converts human-friendly commands into computer instructions. This means that it takes human-readable code as input and then interprets the code into machine language. In a sense, other computer languages involve a similar process; however languages like C/C++ or Fortran are much more efficient at it. But, those languages are categorized as compiled languages because they are converted to machine code once the compilation process is complete. Python programs are analyzed by the interpreter “on the fly”, which causes Python to run much slower. Luckily, hardware and software (OS) improvements have been so dramatic over the past 30+ years that the hit to performance is not as noticeable. The advantage to coding in an interpreted language is that it is easier to tweak and debug because the variables are stored in local memory and there is no need to re-compile with every change.
Additionally, Python can be easily run from the command-line, which allows users to experiment with Python commands without having to create a fully fledged program. For this course, we will make use of Jupyter notebooks, which are similar to notebooks in Mathematica. In the previous chapter, we experimented with storing variables and creating a numpy array. Python can be used for arithmetic tasks as well. Try this:
x = 4
y = 16
x*y
64
In the above lines, the notebook stores the integer (int) 4 into memory and gives it a label x, where in the second line a similar action is performed where the label is y. Under most conditions, Python will assume the number is an 64-bit integer when there is not a decimal point. The product of two integers is also an integer and hence, the operation x*y returns 64 as an integer.
x**y
4294967296
An integer raised to an integer power (Note: Python uses ** for exponents instead of ^) is simply the repeated product of integers. Therefore x**y is equivalent to \(4^{16}\) and Python returns a large integer. The division of two numbers can sometimes be confusing for the interpreter and can depend on the version of Python. In the past, the division of two integers would return an integer (e.g., \(4/2 = 2\)), but what would happen for 2/4?
y/x
4.0
A good practice is to use the decimal point during multiplication or division. This removes the ambiguity for the interpreter and forces it to return a floating point number (float). For example:
int(2/4)
0
2./4.
0.5
You may be asking where this might be important. Python includes a function for square root (e.g., \(\sqrt{x}\) = sqrt(X)), but not for higher roots. Some Python (and C) programs will change 1/3 from a cube root into 0 (e.g., \(3^{1/3} \rightarrow 3^0\)) and return 1.
2.3. Simple Input & Output#
In the previous chapter, we read from a file using the genfromtxt function from numpy, but you may want to take in some user input “on the fly”. This can be accomplished using the input function, where you will need to designate a variable to store the user input. For example:
name = input("What is your name?")
print(name)
Arthur, King of the Britons
quest = input("What is your quest?")
print(quest)
To search for the Holy Grail
airspeed = input("What is the airspeed of a laden swallow?")
print(airspeed, type(airspeed))
100 <class ‘str’>
Notice in the above examples that input stored the user input as a string of characters (string or str).
Output can be directed to a file or the command prompt. For the command prompt, you can print stored variables using the print function. To determine the data type of a stored variable, use the type function. Note: that type can return datatypes like ndarray for numpy array as well as string, int, or float.
Printing variables isn’t limited to strings, but can be useful for probing numerical variables when debugging your code. For example, you might think your code is doing one thing, when in fact it is doing something else entirely. Python borrows a print syntax that is similar to the one used in C/C++ programs. Let’s look at the value of \(\pi\).
import numpy as np
pi = np.pi
print(pi)
3.141592653589793
In the above code, we imported the numpy module and gave it a label np for easier referencing. Then, the value of \(\pi\) from numpy was stored as a float in the variable pi. Finally, \(\pi\) was printed in machine (or double) precision (15 decimal places). Note that some versions of Python default to single precision (8 decimal places).
Maybe we want to know \(\pi\) to a four decimal places, as an integer, or in scientific notation. Then we can use the following:
"Pi to 4 decimal places is: %1.4f" % pi
'Pi to 4 decimal places is: 3.1416'
"Pi as an integer is: %d" % pi
'Pi as an integer is: 3'
"10*Pi to 8 decimal places, but in Scientific Notation is: %1.8e" % (10*pi)
'10*Pi to 8 decimal places, but in Scientific Notation is: 3.14159265e+01'
Some of the common string formatting indicators are:
Format |
Description |
|---|---|
%xd |
Integer value with the total width x |
%x.yf |
Floating point value with a pre-allocated width x and y decimal places. Note the total width will be expanded so that it includes the decimal places and the decimal point can count towards the total width. |
%x.ye |
Scientific (exponential) notation with the total width x and y decimal places. |
%xs |
String of characters with total width x |
Python 3 introduced a new way to format strings using the format function. Let’s use the example that 6 bananas cost $1.74
print('{0} {1} cost ${2}'.format(6,'bananas',1.74))
6 bananas cost $1.74
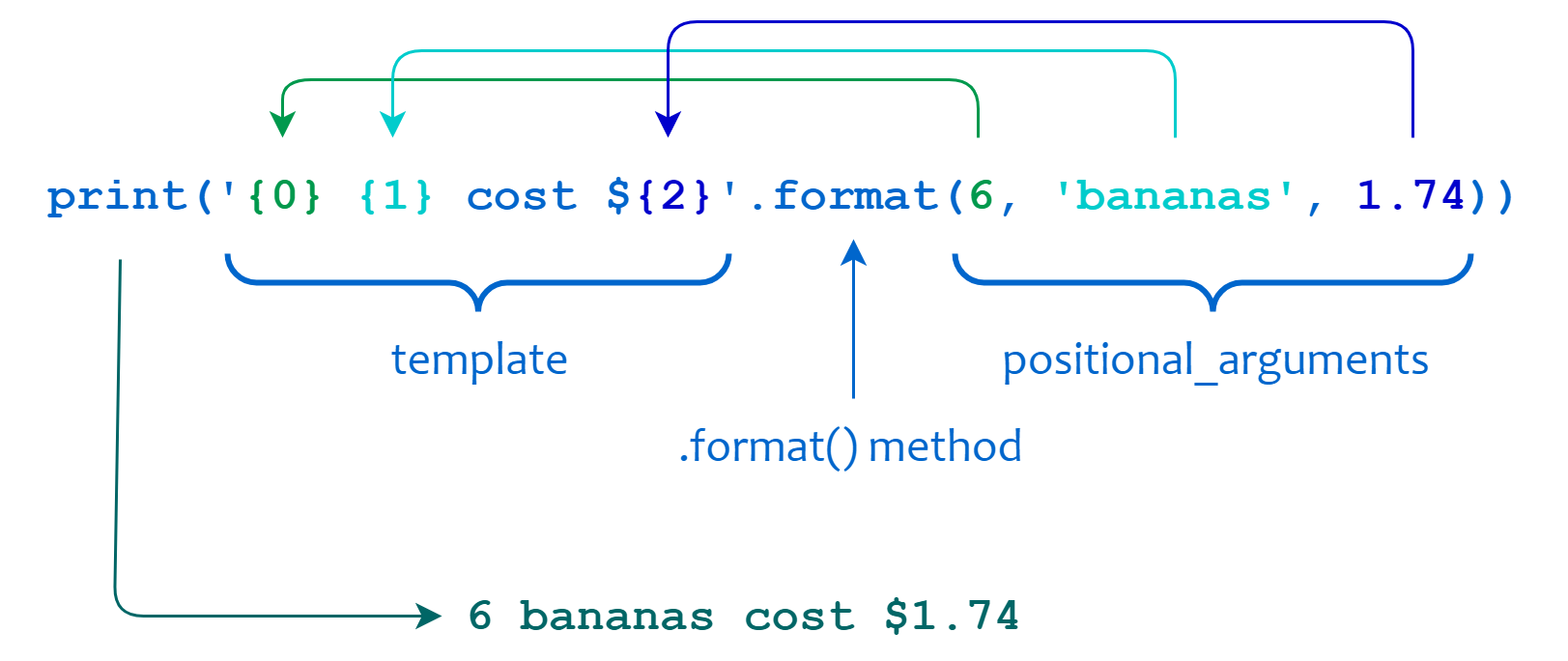
Fig. 2.1 Example taken from realpython.com#
We can obtain the same functionality in defining the number formatting using :x.yf after the position in the {} of the format template.
print('{0:1d} {1} cost ${2:1.2f}'.format(6,'bananas',1.74))
6 bananas cost $1.74
2.4. Variable Types#
Thus far, I hinted at the different types of variables in Python. Those are the typical variables that exist in all programming languages. However, there are two broad divisions in variable types in Python:
numeric types, which hold a single number, such as an integer, floating point number, or a complex number (e.g., \(2-3i\)), and
sequence types, which hold multiple objects (imagine a filled grocery bag) that could be single numbers, characters, or even collections of different things.
Numeric Types
Integer: The integer is the simplest numeric type in Python. They are useful for counting items or tracking indices in an array. The maximum 32 bit integer is \(2^{31} - 1 = 2,147,483,647\)
Long Integer: Integers larger than \(2^{31} - 1\) are stored automatically as long integers. When you use the
typefunction on them, there is a trailingLto indicate it is a long integer.Float: The floating point type is a number containing a decimal point. Floats require more memory to store and are slower in calculations. Python upconverts variable types (recall the \(1/2 = 0\) vs \(1./2 = 0.5\) distinction).
Complex: Complex numbers are naturally included in Python, but uses \(j\equiv\sqrt{-1}\). For example, \(x=0.5+1.2j\) is a valid complex number.
Sequence Types
Tuple: Tuples are indicated by parentheses
(). Items in tuples can be any other data type, including other tuples. Tuples are immutable, meaning that once defined their contents cannot change.List: Lists are indicated by square brackets
[]and are almost the same as tuples. However, lists are mutable: individual items in a list can be changed.String: A string is a sequence of characters. Strings are surrounded by either double
"or single'quotes. Strings are immutable (like tuples), but can only include characters.Reserved characters: Some characters are reserved (like
#for comments), but can be used with an escape\.Tab and Newline: To indicate a
tabcharacter, use an escape\+t(\t). A similar approach is used for a newline (\n).
Dictionary: Dictionaries are indicated by curly brackets
{}. The are different because they use “keys” (which are string labels) instead of numeric indices. Dictionaries are useful when managing data, where you want to assign the column header of a table as the key instead of referencing the column index.
Here are some examples of sequence types
Pythons = ("Cleese", "Palin", "Idle", "Chapman", "Jones", "Gilliam")
#Note that the index counting begins from zero and counting can be startied \
# from the end of the type using negative numbers (starting from 1)
print(Pythons[0],Pythons[2],Pythons[-1])
#One can also specify a slice of a sequence, where slices start on the first\
# index : terminate when reaching the second index (but do not include it)
print(Pythons[1:3])
#Let's see what happens if we try to replace an element of a tuple
Pythons[1] = "Atkinson"
Cleese Idle Gilliam
('Palin', 'Idle')
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
<ipython-input-17-f858c09af6dc> in <module>
9
10 #Let's see what happens if we try to replace an element of a tuple
---> 11 Pythons[1] = "Atkinson"
TypeError: 'tuple' object does not support item assignment
Python errors are usually more descriptive that in other programming languages. A TypeError occurs when you have tried to an action, but it is forbidden due to the data types involved. In the above example, Pythons is a tuple, which is immutable and thus, can’t be changed after it is defined. Line 11 attempts to replace Palin with Atkinson, but this isn’t allowed and hence, the error message.
print("Pythons is a tuple and immutable; Let's change it to a list with []")
Pythons = ["Cleese", "Palin", "Idle", "Chapman", "Jones", "Gilliam"]
#Let's see what happens if we try to replace an element of a list
Pythons[1] = "Atkinson"
print(Pythons)
Pythons is a tuple and immutable; Let's change it to a list with []
['Cleese', 'Atkinson', 'Idle', 'Chapman', 'Jones', 'Gilliam']
Another example is creating a 2-dimensional array or matrix
matrix = [[1,2,3],[4,5,6],[7,8,9]]
#matrix is list of lists, where each row is its own list (columns)
print(matrix)
[[1, 2, 3], [4, 5, 6], [7, 8, 9]]
Think about how to reference values constructed as a list of lists like matrix. How can we reference the value 5 in the matrix? (Remember that indices start from zero!)
matrix[1]
[4, 5, 6]
print(matrix[1][1])
matrix[1][1] = 0
print(matrix[1][1])
5
0
This type of list construction requires the [i][j] method of indexing and it applies to tuples of tuples as well. This is a little clumsy, where we it would be clearer to have [i,j] indexing, where i=>row and j=>column. This can be accomplished by converting matrix from a list into a numpy matrix.
Note
Recall that the numpy module was loaded earlier in the notebook when converting strings. If you run into trouble, you may need to add import numpy as np at the top of your notebook.
matrix = np.matrix(matrix)
print(matrix)
#Notice that the commas have been removed and the matrix starts \
# looking like a more traditional matrix
print("The element in the 0th row and 2nd column is: ",matrix[0,2])
[[1 2 3]
[4 0 6]
[7 8 9]]
The element in the 0th row and 2nd column is: 3
2.4.1. Sequence Tricks#
If you are needing to store of N numbers, but don’t know the values beforehand. Here are two ways:
Create an empty list with the needed length
Create an empty array filled with ones/zeros
N = 5
LongList = [None]*N
LongList[3] = np.pi
print(len(LongList),LongList)
LongList = np.zeros(N) #Note that this overwrites the previous variable
LongList[2] = np.pi/2
print(len(LongList),LongList)
5 [None, None, None, 3.141592653589793, None]
5 [0. 0. 1.57079633 0. 0. ]
where it depends on what you want to store. Approach #1 would be more useful if you were storing strings or different data types. Sometimes you may not know exactly how many list elements you need until after the fact. Elements can be added to the end of a list using the [list_name].append() function. Here’s an example:
Values = []
print(Values)
#Some calculation is done and you need to store NewValue into the Values list for later
NewValue = 4
#The append function acts on the list object *Values* and takes the NewValue as input
Values.append(NewValue)
print(Values)
[]
[4]
Notice that we started with an empty list. In this case appending to it just adds one element. Go back and fill Values with a few numbers. Then re-run the cell. Now you can see the NewValue is indeed added to the end of the list.
Another handy trick is sorting. There are two types of sorting:
in-place (sort) or
return (sorted).
In some cases you may want to sort a list but also want to preserve the original list; this is where the second option becomes useful. Luckily, these two options are implemented differently to help distinguish between them. The sort function acts on a list object, where the sorted function takes the list as an argument (input) to return.
ValueData = [5,3,7,6,2,7,2,9,4,0]
StringData =["Tommy","Dick","Harry","Sally","Mary","Nina"]
New_ValueData = sorted(ValueData) #returning the sorted list into a new variable
print("The original list: ",ValueData)
print("The sorted list: ", New_ValueData)
ValueData.sort()
print("Sorting in-place using sort: ",ValueData)
StringData.sort()
print("Sorting strings in-place: ", StringData)
ValueData[4] = StringData[3]
print("Replacing an element of ValueData with a string: ",ValueData)
The original list: [5, 3, 7, 6, 2, 7, 2, 9, 4, 0]
The sorted list: [0, 2, 2, 3, 4, 5, 6, 7, 7, 9]
Sorting in-place using sort: [0, 2, 2, 3, 4, 5, 6, 7, 7, 9]
Sorting strings in-place: ['Dick', 'Harry', 'Mary', 'Nina', 'Sally', 'Tommy']
Replacing an element of ValueData with a string: [0, 2, 2, 3, 'Nina', 5, 6, 7, 7, 9]
The last two lines mixed the data types so that a string is now in the list of values. Do you think a sort will work?
2.4.2. Iterables#
Python allows for special functions called iterables that can contain the instructions to generate a list without allocating the memory. A common iterable is the range function, which generates a list of integers given three parameters: starting value, stopping value, and increment (must be an integer). This is especially useful if you need to quickly generate a range of indices for a process or array.
#Create a list of 100 numbers for a graph axis
axis = list(range(0,100))
print(axis)
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99]
#Create a list of even numbers from 6 up to 17.
Evens = list(range(6,17,2))
print(Evens)
[6, 8, 10, 12, 14, 16]
We often need a more flexible means of generating a list of values. Suppose that we want to generate a list of floating point numbers. The previous trick can be modified.
axis = [0.02 * i for i in range(0,100)]
#Only printing the first 10 values for this example
print(axis[:10])
#Another way is to use the **arange** function from numpy, \
# where the difference is whether you need a list or array returned
np_axis = np.arange(0,100,0.02)
print(np_axis[:10])
[0.0, 0.02, 0.04, 0.06, 0.08, 0.1, 0.12, 0.14, 0.16, 0.18]
[0. 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16 0.18]
Lists can become iterables themselves too.
new_axis = [a*10 for a in axis]
print(new_axis[:10])
#Notice that some values are not exact.
#Axis was stored in memory as floating point numbers with \
# limited precision
#Iterating over floats like this can generate some \
# unexpected results due to the limitation of numerical precision
[0.0, 0.2, 0.4, 0.6, 0.8, 1.0, 1.2, 1.4000000000000001, 1.6, 1.7999999999999998]
2.5. Mathematical Operators#
Thus far, you have seen typical arithmetic operators + - * / on numerical values. However, these operators don’t work the same way with lists. The + operator for two lists does not add them together, rather it concatenates them (i.e., joins the lists). A similar process occurs with strings because they are lists of characters. The * operator makes copies of lists instead of multiplying the elements.
Division / has a few quirks, where it works fine for floats. But it does third-grade math for integers (i.e., the result is the integer portion of the actual answer). There are instances when you might want the third-grade math behavior for floats, in which case you can use the floor division // operator. At the beginning of this chapter, you saw that ** is responsible for exponentiation. The modulo operator % returns the remainder, although it is also used for string conversions.
#Examples of Operators
String_a = "Jack and Jill"
String_b = " went up the hill"
print(String_a + String_b) #Concatenation of strings using +
List_a = ["Jack","and","Jill"]
List_b = ["went","up","the","hill"]
print(List_a+List_b) #Concatenation of lists using +
print(10//4)
print(2**4)
remainder = 10 % 3
print("Remainder of 10 % 3 is: ",remainder)
Jack and Jill went up the hill
['Jack', 'and', 'Jill', 'went', 'up', 'the', 'hill']
2
16
Remainder of 10 % 3 is: 1
There are also some shortcut operators, that help reduce the amount of code. Suppose you want to increment a counter. The += operator is a shortcut for when you want to perform an addition and immediately replace the value stored in the variable.
Similar operators exist for other arithmetic operators as *=, /=, or -=. These operators are best for people to generate code more quickly, but do not affect the speed of the code. Sometimes they make the code harder to read by others, so use them cautiously.
#Create a counter and increment it
counter = 0
print("The initial value is ", counter)
counter = counter + 1 #this is the long way
print("The next value is ", counter)
counter += 1 #this is the short way
print("The next value is ", counter)
The initial value is 0
The next value is 1
The next value is 2
2.6. Lines in Python#
Python uses spaces and indentation as part of the syntax. This is in contrast to C/C++, Fortran, or JAVA that use (), {}, or ; to separate out bits of code. The Python interpreter actually cares about blank spaces before commands on a line. As a result, there are two types of lines:
physical lines (number of lines in the code) or
logical lines (number of lines executed in the code).
#Show the differences between a physical line and a logical line
x = "This line is a physical line and a logical line"
print(x)
x = x.split() #The split function helps split a string into a list
print(x)
#Note that the \ at the end of a line creates a soft line \
# break (i.e., breaks the physical line, but not the logical one);
x = "this line is multiple\
physical lines but is\
just one logical line"
print(x)
x = x.split()
print(x) #Notice that split removes the extra spaces
This line is a physical line and a logical line
['This', 'line', 'is', 'a', 'physical', 'line', 'and', 'a', 'logical', 'line']
this line is multiple physical lines but is just one logical line
['this', 'line', 'is', 'multiple', 'physical', 'lines', 'but', 'is', 'just', 'one', 'logical', 'line']
2.7. Control Structures#
Control statements direct or modify the flow of logic within a program thereby allowing the program to be flexible depending on what happens. For example, “If you are hungry, then eat lunch” is a control statement. Control statements require a conditional (boolean=True or False) to evaluate before taking an action. Most control statements have a clear end point, where while does not (be careful with while loops).
Conditionals
A conditional is anything that can be evaluated as either True or False. In Python, the following things are always False:
The word False (note the capitalization)
0,0L, or0.0""or''(an empty string)(),[], or{}(an empty sequence)
Almost everything else is True:
1,3.14,42(True because they aren’t zero)The word True (note the capitalization)
"False","0", or[0,False,(),""](Why are these true?)
Conditionals have operators to evaluate the relationship between objects, which may be True or False.
<Less than>Greater than<=Less than including equal to>=Greater than including equal to==Equal to (avoid using equal for comparing floats)!=Not equal to
Note that = is an assignment (i.e., store something to a variable), where == is a conditional (i.e., are two objects congruent). This is one of the most common bugs in Python programs, where an = is missed. There are also the boolean operators and, or, in and not.
Name = input("What is your name?")
Cast = Pythons
if Name in Cast:
print("Yes, ",Name," is a member of Monty Python")
else:
print("No, you're an impostor!")
No, you’re an impostor!
In the above example, there are two print statements. Depending on the user input stored in Name, a different print statement is evaluated. This demonstrates the most basic control statement if...else. Often we generate (thought) examples using pseudocode, which uses plain language and generally follows the language syntax. An example of a control state (in pseudocode) is:
if (Check if these are the droids you're looking for): #The colon (:) signifies the end of a conditional
Grab them
elif (These might be them): #Check another condition, maybe there are many
Ask your superiors
else: #Finally after checking everything else
Fall for the Jedi mind trick
Go about your business, move along
Python uses the indentation to determine where the conditional ends, so the non-indented lines are executed after the conditional statements are checked. In other computer languages, indentation is used to make the code easier to read; but the is a defining trait in Python. The indentation is not optional.
The while statement is used to repeat a block of commands until a condition is met. The most common example is the instructions given on shampoo.
while (in the shower):
extract shampoo from bottle into hand
apply to hair
lather
rinse
In this statement, the instructions are given while while the condition (in the shower) is True and repeated until the condition is False. Notice that there is not a conditional to indicate when to stop. This is a common bug for new programmers, which results in an infinite loop and is most profitable for the shampoo manufacturers. A proper while loop has the following structure:
while (in the shower):
extract shampoo from bottle into hand
apply to hair
lather
rinse
if (hair is clean):
get out of the shower!
There are a few keywords that can be used in conjunction with a while loop.
pass: Thepasskeyword does nothing. Its purpose is to take up a line if there is a structural need for one. Sometimes you have a conditional fordo somethingornothing.continue: Thecontinuekeyword moves the program execution back to thewhile(i.e., excludes the lines that come after and increments the loop)break: Thebreakkeyword moves the program execution to outside thewhile(“breaks out”).else: Theelsecommand delineates a block of code that is executed only after thewhileblock executes normally (no breaks).
Here is an example, where the user input value is 237:
#Create a Python program to determine whether a number is prime.
# DISCLAIMER: This is not the most efficient way
Number = int(input("What integer do you want to check?")) #need to make sure input is an integer
divisor = 2 #Use this to set floor on numbers to check
#Main loop to test each number
while divisor < Number:
if Number % divisor == 0: #if remainder is zero then Number is divisible by the number in divisor
print(Number," is divisible by ",divisor, " and thus, not prime")
break #since the number is not prime, we can stop (break out)
else:
#The remainder is not zero, we need to check another divisor
divisor += 1
else:
#all the possible divisors were checked and failed
#must be prime
print(Number," is a prime number")
237 is divisible by 3 and thus, not prime
Sometimes iterating over a sequence is very straight-forward. In that case, the for loop is the way to go. The most basic syntax is:
#Item is a value within the Sequence (number, string, row of a matrix, etc.)
for Item in Sequence:
Do something with Item
After executing the lines within the for loop, the next Item will be the next value in the Sequence. The most common for is for i in range(start,stop):, where the range function generates the sequence and i is simply the index within the range. Make sure that the Sequence is not being changed within the for loop.
2.8. Functions#
2.8.1. Defining a function#
A function is a bit of code that you want to use more than once. It can be a calculation, such as find the distance between two points, or it could be an action like draw a graph or save some data to a file. Functions are defined using def and the function name must start with a letter, while the rest of the name can be composed of numbers, letters, or underscore. After the function name, there is a set of () that contains a list of input variables that are passed to the function. The def command should end with a colon :. The lines following the def command are an indented block and non-indented lines (relative to the def command) are outside the function.
Generally, the first line of a function is a comment block that describes the use of the function, including any assumptions for the input variables (e.g., type, format). A function can return a value, but this is not required and depends on the inheritance of variables. The return value can be numerical or a boolean (True or False).
#Write a function that calculates the factorial of a positive integer
def factorial(n):
"""
This function calculates n! by the simplest method imaginable
n: input integer
f: return value
"""
f = 1 #the smallest factorial is 1
for i in range(2,n+1): #starting from 2 and stopping at n
f *= i
return f
#Now that the function is created, you can call on it anytime you need to know the factorial of a number
print("%2s %7s" % ('n','n!'))
for j in range(0,10):
print("%2d %7d" % (j,factorial(j)))
n n!
0 1
1 1
2 2
3 6
4 24
5 120
6 720
7 5040
8 40320
9 362880
Functions are often used to reduce the code needed to illustrate the big picture and make it more understandable. You are the boss and you delegate tasks to the functions because the boss can’t do everything. Your morning might look like this:
if (Time>=Morning):
GetUp()
GetDressed()
EatBreakfast(Spam,eggs,Spam,Spam,Spam,Spam,bacon,baked_beans,Spam)
else:
ContinueSleeping()
The functions GetDressed() and EatBreakfast() typically entail many actions (i.e., quite a bit of code); but writing them as separate functions allows one to bury the details. Writing the program as a set of functions gives you a modular flexibility (i.e., easy switching for the order of functions). The variables that are passed into the function only exist while the function is active (i.e., local variables).
#Here's the function definition
def sq(x):
#returns the square of a number x
x *= x #this step is to show that x is replaced locally
return x
#Here's the main program
x = 3 #first definition of x
print("x^2 = ", sq(x)) #the return squared value is printed
print("x = ",x) #the value of x is printed
x^2 = 9
x = 3
Note that the local value of x is changed within the function, but the global value of x is not changed in the main program. The reason is that the function stores the value of x as a separate copy in memory but uses the same label for the copy.
Functions can have default values built-in, which is handy when on specific parameter doesn’t change too much. This is done by putting the value directly into the definition line, like this:
def answer2everything(A=42):
return A
#main program
print(answer2everything("How many roads must a man walk down?"))
print(answer2everything())
How many roads must a man walk down?
42
At this point, it should be clear that local variables are in use locally. If a Python function can’t find the value of some variable, it looks outside the function. This is handy: you can define some constants at the beginning of the program and call upon them whenever they are needed. This is in contrast to older versions of Fortran that required you to carry the variables around and pass to each function. Values used throughout the program are called global variables.
What happens in the function, stays in the function. At least most of the time. There are occasions where you might want to change a value globally, in which case refer to that variable in the function as a global.
a, b, c = 4, 5, 6
def fn(a):
d = a #local copy of the value a that is passed in
a = b #the global value b replaces a
global c #this defines c as a global variable
c = 9 #this changes the value of c everywhere
print("initial values ",a,b,c)
fn(b) #passing in the value of b into the fn (d=a=b=5 inside fn)
print("values after function call ",a,b,c) #What will these values be?
#Can we print d here?
print(d)
initial values 4 5 6
values after function call 4 5 9
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
<ipython-input-41-f839ccca5d1a> in <module>
11
12 #Can we print d here?
---> 13 print(d)
NameError: name 'd' is not defined
2.8.2. Passing functions#
Python treats functions just like any other variable. This means that you can store function in other variables or sequences. Even passing functions into other functions is allowed.
"""
pass_trig.py
Demonstrates Python's ability to store functions as variables and pass those functions to other functions
--Assumes that 'import numpy as np' has been called
"""
import matplotlib.pyplot as plt
def plot_trig(f):
#plots the function f over the range(-pi,pi)
xstep = np.pi/20.
xvals = np.arange(-np.pi,np.pi+xstep,xstep)
ax.plot(xvals,f(xvals),'-',lw=2)
trig_func = (np.sin,np.cos,np.tan) #a tuple holding some trig functions
fig = plt.figure()
ax = fig.add_subplot(111)
for func in trig_func:
#for each trig function test a value and plot a graph
print("function value at pi/6 is: ",func(np.pi/6))
plot_trig(func)
ax.set_xlim(-np.pi,np.pi)
ax.set_ylim(-2,2)
fig.savefig("Trig_pass.png",bbox_inches='tight',dpi=300)
function value at pi/6 is: 0.49999999999999994
function value at pi/6 is: 0.8660254037844387
function value at pi/6 is: 0.5773502691896257
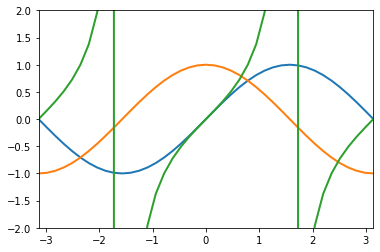
The functions in this example are stored in a list, referred to as elements in lists, and passed to other functions.
2.9. Program Structure#
Python programs allow for a lot of flexibility, which is one of its strengths. However, this much freedom can also be a source of confusion. When we develop a program, we must employ some convention to make it easier for others to read and/or use. This is similar to how we choose to write from left to right or drive on the right side of the road (those silly Brits). As a result a common program structure is as follows:
#Program title
#short description
Import block #all import statements (numpy,scipy,matplotlib,etc.)
Define constants #defining physical constants like G, k, c, etc.
Function block # define each function (preferably in alpha order)
Main program #this is where the magic happens
Program end #sometimes you need to close the opened objects (files, figures, processing pool, etc.)
2.10. Problems#
Complete the following problems in a Jupyter notebook, where you will save your results as an external file (*.png).
Create a \(\LaTeX\) document with:
an abstract summary
sections for each problem that state the problem, explain your approach to solving the problem, and display the results
include a reference for each solution (this can be textbooks)
Problem 1
Create a list holding the squares of the numbers between 10 and 20, including the endpoints.
Problem 2
Write a Python program to print out the first N number of the Fibonacci sequence, where N is provided by the user and is greater than 2.
Problem 3
Write a Python program that creates two lists (time and height) for a projectile thrown vertically at some initial velocity \(v_i\). The program should ask the user for the initial height \(y_i\) and velocity \(v_i\), and produce a table containing 50 data points over 5 seconds.
Problem 4
The energy levels for a quantum particle in a 3D rectangular box of dimensions {\(L_1\), \(L_2\), and \(L_3\)} are given by:
Write a program that will calculate, and list in order of increasing energy, the n’s for the 10 lowest different energy levels, where \(L_2 = 2L_1\) and \(L_3 = 4L_1\). Note: it may be easier to print the results using units of \(\frac{\hbar^2\pi^2}{2m}\).
Problem 5
Write a function that calculates the value of the nth triangular number. Triangular numbers are formed by adding a series of integers {1,n} (see triangular numbers).
Problem 6
Write a Python program to make an \(N \times N\) multiplication table and write this table to a file. Each row in the table should be a single line and tab-delimited. The program size of the table and the filename should be supplied by the user.


2.2. Comments#
Every programming language allows for the programmer to leave notes (or comments) within the code. Adding comments to your code is very important because
You and future you need to communicate; It is not uncommon to write some code and comeback to it more than 6 months later. After which, some unkind words maybe directed at past you from yourself for not leaving comments.
The future person to read the code may not be future you and they will not know what you were thinking.
Comments can be designated with the
#(hashtag) symbol, where the text that follows it is ignored by the interpreter until the next line. However this can be impractical if you are providing a description of a function that takes many lines. In this case, three'''(apostrophe) symbols are used to begin a block comment, where another three'''symbols are needed to end the block comment. Otherwise, the interpreter will either return an error or not do anything at all.